この記事では、Python言語とNumPyを用いて、最小二乗法で線形近似で求める方法をソースコード付きで解説します。
最小二乗法
最小二乗法とは、データの組(X, Y)を、関数を用いて近似する手法の1つです。
残差の二乗和を最小とするように関数の係数を求めることから最小二乗法と呼ばれます。
PythonとNumPyのlinalg.lstsqを利用すると、連立方程式の解を求めることが出来ます。
書式
a,b = linalg.lstsq(A,Y)[0]
第1引数(A)：行列A(Xに右から単位行列を結合した行列)
第2引数(Y)：データ群(X, Y)のうちのベクトルY
戻り値(a,b)：最小二乗法で求めた近似直線の傾きと切片
処理手順
①科学計算モジュールNumPyをインポートする。
②データXを定義する。
③データYを定義する。
④linalg.lstsqで最小二乗法をおこない、近似直線の傾きaと切片bを求める。
⑤計算結果を表示する。
ソースコード
サンプルプログラムのソースコードです。
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def main():
X = [1,2,3,4,5]
Y = [1.1, 2.1, 2.8, 4.3, 5.1]
A = np.array([X,np.ones(len(X))])
A = A.T
a,b = np.linalg.lstsq(A,Y)[0]
plt.plot(X,Y,"ro")
plt.plot(X,(a*X+b),"g--")
plt.grid()
plt.show()
if __name__ == '__main__':
main()
実行結果
サンプルプログラムの実行結果です。
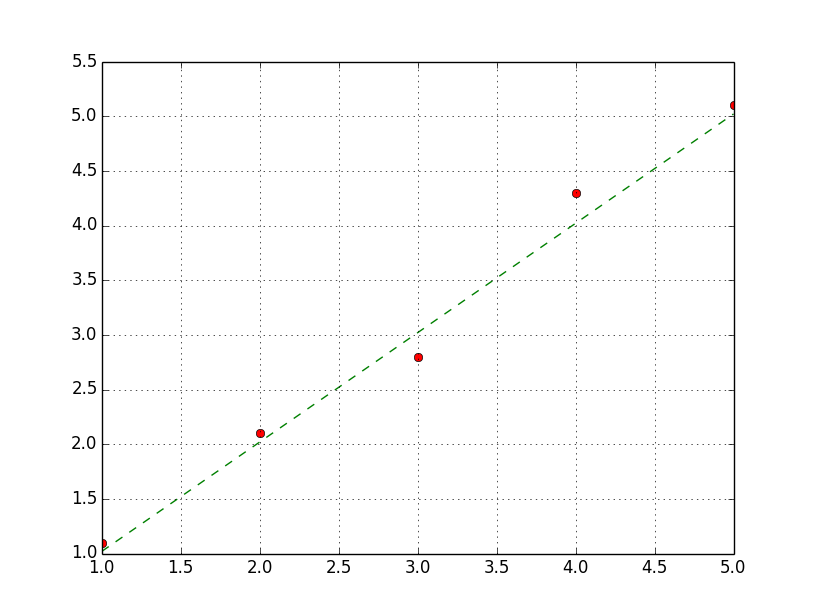
データ(赤点)に対して近似直線(緑の破線)が引かれています。
コメント