Pythonライブラリ「yfinance」と「matplotlib」をを使用してオルカン(All Country World Index)とS&P 500の過去5年間の価格を取得し、データを正規化してグラフで比較する方法を解説します。
サンプルコード① S&P500とオルカンのデータをグラフ化
Pythonとyfinanceライブラリを使用してオルカン(All Country World Index)とS&P 500の過去5年間のデータを取得し、matplotlibライブラリでグラフ化して比較します。
yfinanceライブラリのインストール方法については「【Python】「yfinance」をpipでインストールする方法」で解説しています。
解説動画
本ページの内容は以下動画でも解説しています。
サンプルコード①
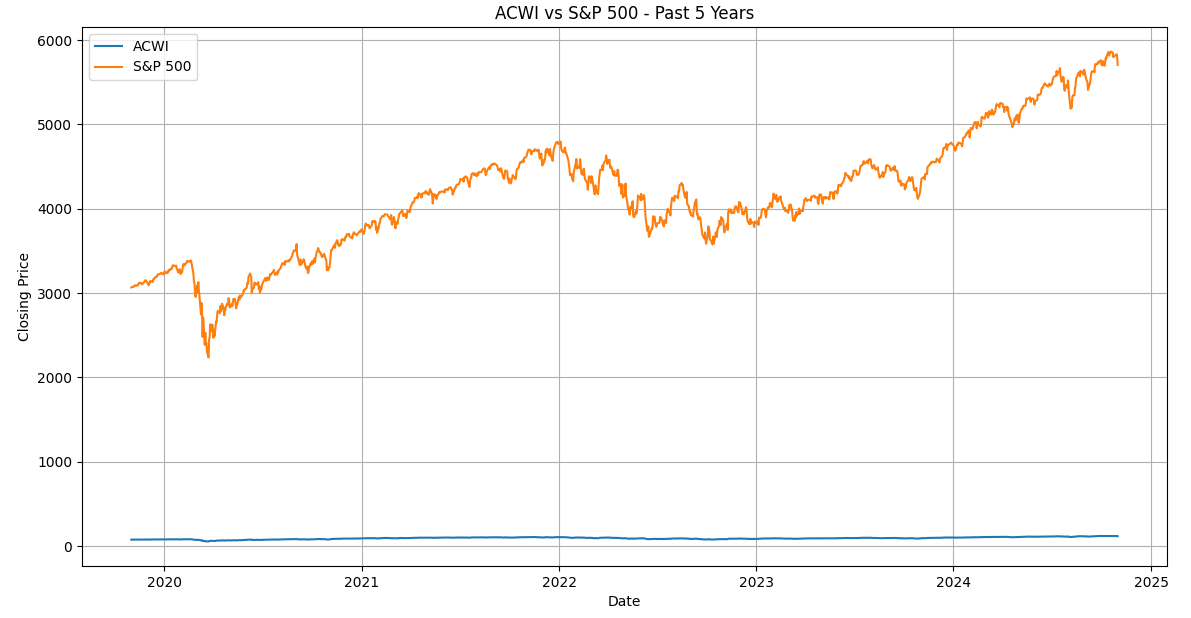
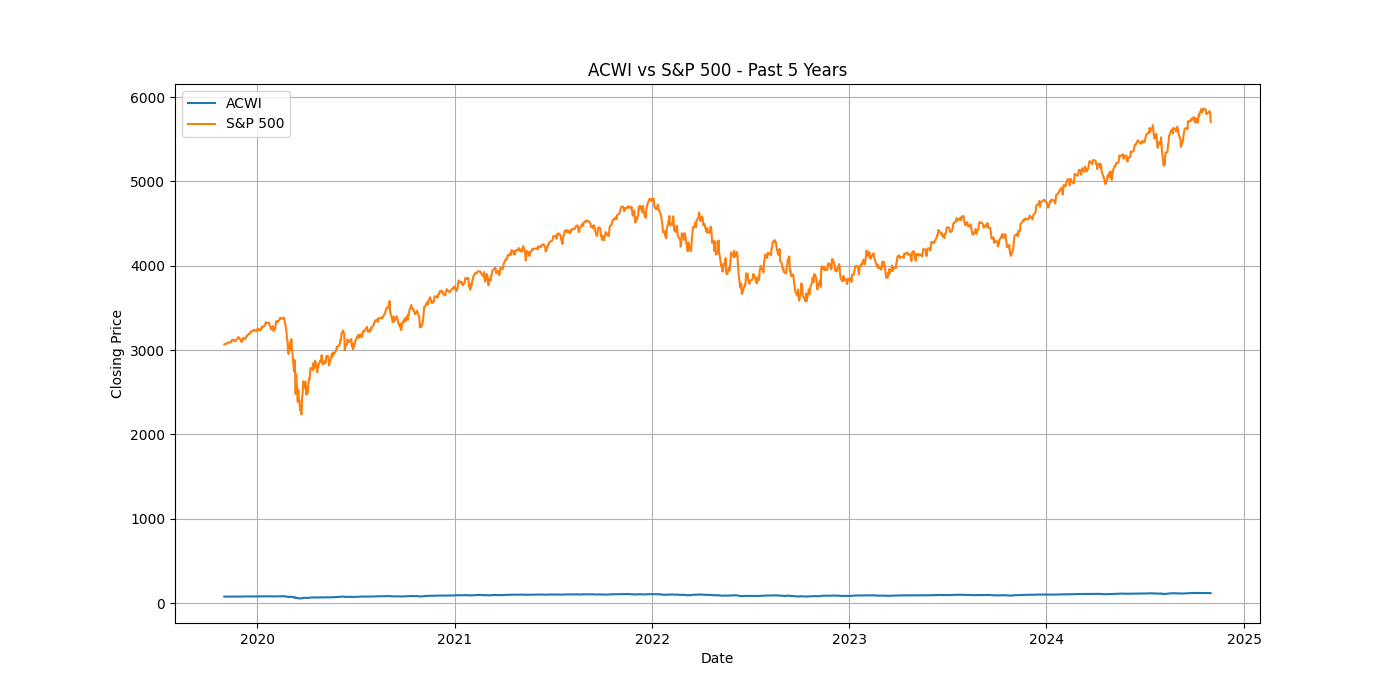
実行結果
横軸が価格(ドル)、横軸が時間です。
オルカンとS&P500は価格差があるので、単純に価格を同じグラフにプロットしただけだと、比較しにくいです。
コード解説
コードの各部分について解説します。
- ライブラリのインポート:
import yfinance as yf import matplotlib.pyplot as pltyfinanceはYahoo Financeから株価データを取得するためのライブラリです。matplotlib.pyplotはデータを可視化するためのライブラリです。
- ティッカーシンボルの設定:
acwi_ticker = "ACWI" sp500_ticker = "^GSPC"ACWIはオルカンのティッカーシンボルです。^GSPCはS&P 500のティッカーシンボルです。
ティッカーシンボルは、株式市場で取引される銘柄を識別するための一意のコードです。
通常、アルファベットの組み合わせで構成されており、各銘柄に固有のシンボルが割り当てられています。例えば、Apple Inc.のティッカーシンボルは「AAPL」、Microsoft Corporationのティッカーシンボルは「MSFT」です。
これらのシンボルを使って、株価情報を検索したり、取引を行ったりすることができます。ティッカーシンボルは、株式市場だけでなく、債券やETF(上場投資信託)などの他の金融商品にも使用されます
- 株価データの取得:
acwi_data = yf.download(acwi_ticker, start="2019-11-01", end="2024-11-01") sp500_data = yf.download(sp500_ticker, start="2019-11-01", end="2024-11-01")yf.downloadを使って、指定したディッカーシンボルと期間(2019年11月1日から2024年11月1日まで)の株価データを取得します。
- 終値の取得:
acwi_close = acwi_data["Close"] sp500_close = sp500_data["Close"]- 取得したデータから、終値(Close)を抽出します。
- グラフの作成:
plt.figure(figsize=(14, 7)) plt.plot(acwi_close, label="ACWI") plt.plot(sp500_close, label="S&P 500") plt.title("ACWI vs S&P 500 - Past 5 Years") plt.xlabel("Date") plt.ylabel("Closing Price") plt.legend() plt.grid(True) plt.show()plt.figure(figsize=(14, 7))でグラフのサイズを設定します。plt.plotでそれぞれの終値データをプロットします。plt.titleでグラフのタイトルを設定します。plt.xlabelとplt.ylabelでそれぞれの軸のラベルを設定します。plt.legendで凡例を表示します。plt.grid(True)でグリッドを表示します。plt.show()でグラフを表示します。
yf.downloadの使い方
import yfinance as yf
# ティッカーシンボルを指定してデータを取得
data = yf.download(tickers, start='2020-01-01', end='2021-01-01')
print(data)
tickers: 取得したい銘柄のティッカーシンボル。「”ACWI,^GSPC”」というように複数のティッカーをカンマで区切って指定することもできます。start: データ取得の開始日(YYYY-MM-DD形式)。end: データ取得の終了日(YYYY-MM-DD形式)。interval: データの間隔。デフォルトは1日。以下の値が使用できます。1m: 1分2m: 2分5m: 5分15m: 15分30m: 30分60m: 1時間1d: 1日5d: 5日1wk: 1週間1mo: 1ヶ月3mo: 3ヶ月
group_by: データをどのようにグループ化するか。デフォルトはticker。auto_adjust: 調整後の終値を自動的に計算するかどうか。デフォルトはFalse。prepost: 市場前後のデータを含むかどうか。デフォルトはFalse。threads: 複数のスレッドを使用してデータを取得するかどうか。デフォルトはTrue。
yf.downloadの戻り値は、指定したティッカーシンボルの株価データを含むPandas DataFrameです。このDataFrameには、以下のような列が含まれます。
- Date: 日付
- Open: 始値
- High: 高値
- Low: 安値
- Close: 終値
- Adj Close: 調整後終値
- Volume: 出来高
サンプルコード② 変動率で正規化してグラフ化
異なる銘柄の株価を比較する際、株価をそのまま比べるよりも正規化(Normalization)したほうが分析しやすくなります。
正規化には複数の種類がありますが、単純なのは「各銘柄の株価を基準日(例えば、比較を開始する日)の株価で割った変動率」を用いる方法です。
基準日での株価が1000円の銘柄Aと100円の銘柄Bがあったとします。
1ヶ月後に銘柄Aの株価が1100円、銘柄Bの株価が120円になった場合、それぞれの株価変動率は以下のようになります。
銘柄A: 変動率=1100円 / 1000円 = 1.1(10%の上昇)
銘柄B: 変動率=120円 / 100円 = 1.2(20%の上昇)
このように、正規化することで、異なる銘柄の株価変動を同じ基準で比較できるようになり、どちらの銘柄がよりパフォーマンスが良いかを判断しやすくなります。
サンプルコード②
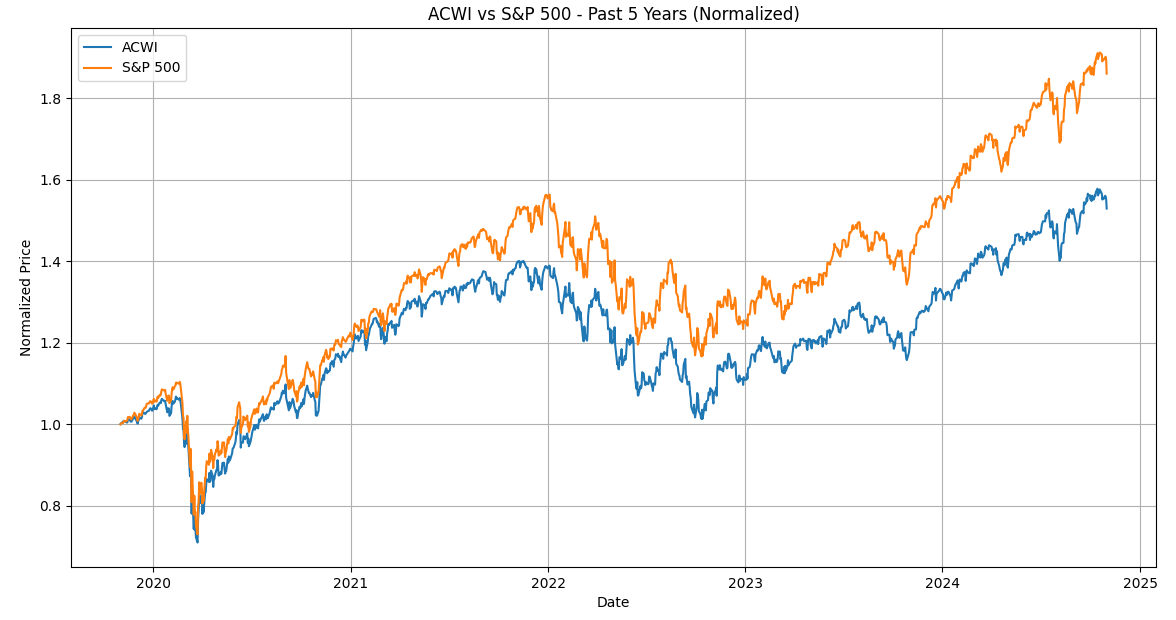
各株価を初期値で割ることで、すべてのデータを1から始まるスケールに変換しています。
上記グラフから、過去5年間の比較ではオルカンよりS&P500のほうが上昇率が高い(リターンが高い)ことがわかります。
また、よく言われていることですが、オルカンとS&P500は連動していることもわかります。
実行結果
サンプルコード③ 0~1で正規化してグラフ化
前回は変動率(初期値で割ることで、すべてのデータを1から始まるスケールに変換)を用いた正規化を紹介しました。
正規化には複数種類ありますが、機械学習でデータを学習させるときは、「データの値の範囲を0~1に揃える」という正規化を行います。
ここでは詳細は述べませんが、データを正規化することで安定した学習や予測精度の向上に繋がります。
サンプルコード③
以下のコードは、オルカン(All Country World Index)とS&P 500の株価データを0~1の範囲に正規化するように修正したものです。
Scikit-learnのMinMaxScalerを使用して株価データを0~1の範囲に正規化しています。
実行結果
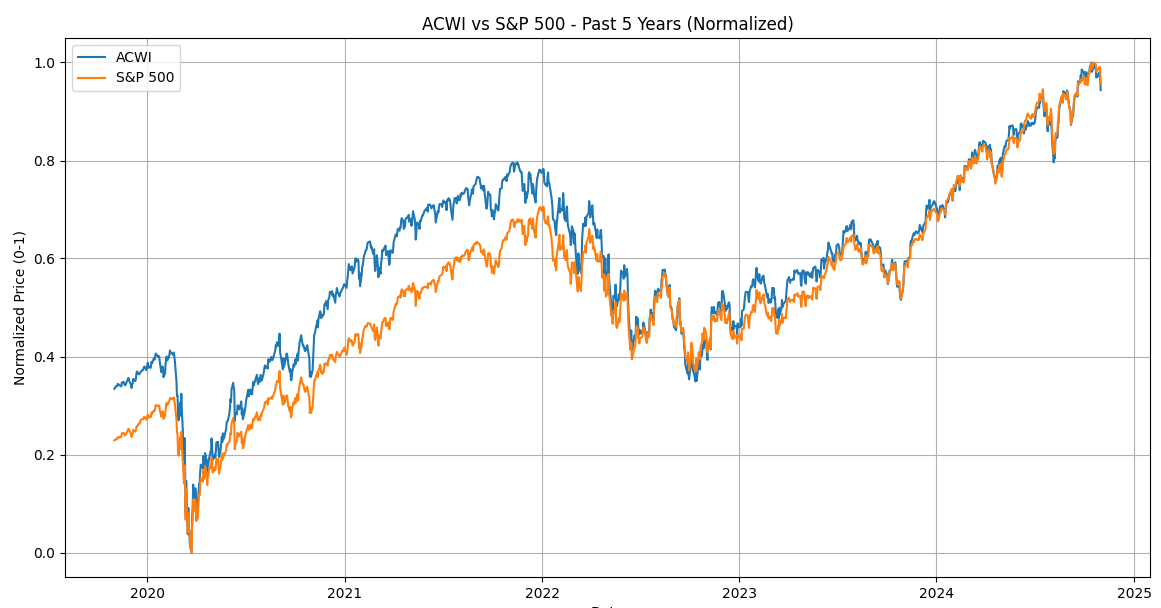
よく言われていることですが、オルカンとS&P500は連動していることがわかります。
サンプルコード④ 0~1で正規化してグラフ化(Scikit-learn無し)
以下のコードは、Scikit-learnを使わずに、サンプルコード③と同様にオルカン(All Country World Index)とS&P 500の株価データを0~1の範囲に正規化し、グラフ化します。
以下が0~1の範囲にデータを正規化するための計算式です。
$ X_{\text{normalized}} = \frac{X – X_{\text{min}}}{X_{\text{max}} – X_{\text{min}}} $
ここで、$X$は元のデータ、$X_{\text{min}}$はデータの最小値、$X_{\text{max}}$はデータの最大値です。
この式を使うことで、すべてのデータが0から1の範囲に収まるようになります。
上記コードでは、この計算をnormalize関数で実装しています。
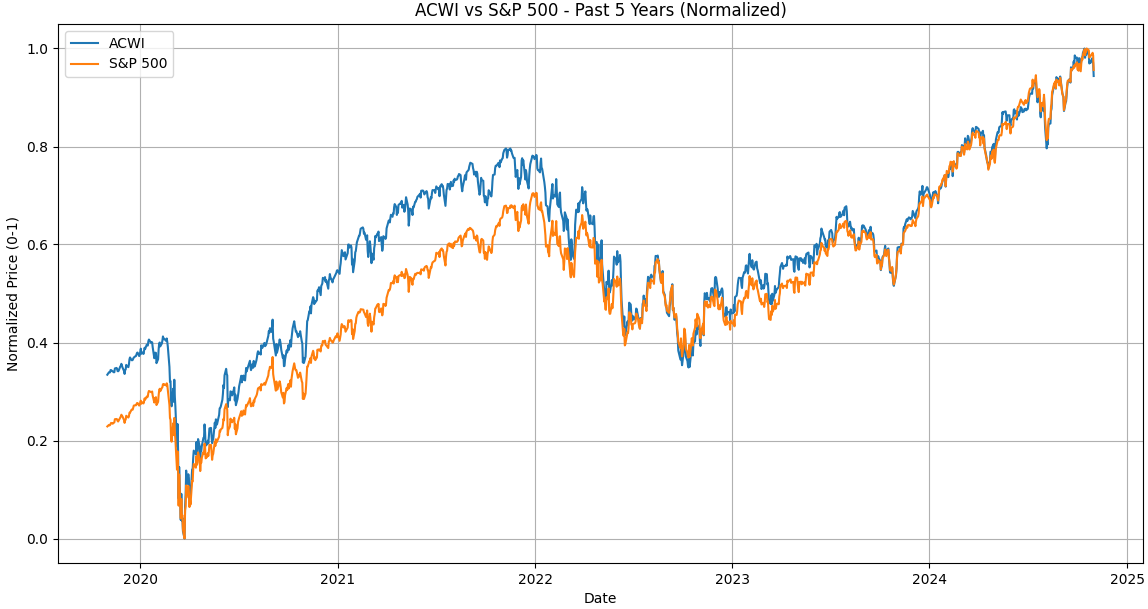
実行結果
関連ページ



コメント