この記事では、Python言語とNumPyを用いて、配列の勾配を求める方法をソースコード付きで解説します。
数値勾配(傾き)
NumPyのgradientを利用すると、簡単に関数の数値勾配(傾き)を計算することが出来ます。
今回は1変数と2変数の関数に対して数値勾配(傾き)を計算しグラフ化してみました。
1変数の書式
np.gradient(y)
2変数の書式
Ey,Ex = numpy.gradient(E ,.2, .2)
第1引数(E):勾配を求めたい関数
戻り値(Ey,Ex):E(x, y)のy方向の勾配とx方向の勾配(順番に注意)
ソースコード
サンプルプログラムのソースコードです。
1変数の場合
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def main():
x = [1., 2., 3., 4., 5.,6. ,7. ,8.]
y = [1., 2., 3., 4., 5.,5.5,7., 9.]
dy = np.gradient(y) # yの勾配を計算
# 結果を表示
plt.plot(x, y, "r-o", label="y")
plt.plot(x, dy, "g-o", label="dy")
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.grid()
plt.legend()
plt.show()
if __name__ == '__main__':
main()
2変数の場合
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
def main():
x = np.arange(0, 10.1, 0.5)
y = np.arange(0, 10.1, 0.5)
(xm, ym) = np.meshgrid(x, y) # グリッドの作成
(xq,yq) = (5, 5) # 電荷の座標
r = np.sqrt((xq-xm)**2+(yq-ym)**2) # 電荷との距離
k = 9.0*10**9 # 比例定数k
q = 1 # 電荷
E = (k*q)/r**2 # 2変数の関数(電場E(x,y)
(Ey,Ex) = np.gradient(E ,.2, .2) # Eの勾配を計算
Ex[Ex>0.5],Ey[Ey>0.5] = 0.5, 0.5 # 勾配の上限下限
Ex[Ex<-0.5],Ey[Ey<-0.5] = -0.5, -0.5
# 結果を表示
plt.quiver(xm,ym,-Ex,-Ey,angles="xy",headwidth=3,scale=20,color="#444444")
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.grid()
plt.legend()
plt.show()
if __name__ == '__main__':
main()
実行結果
サンプルプログラムの実行結果です。
1変数の場合
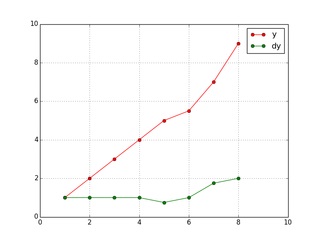
2変数の場合
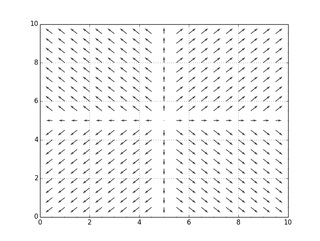

コメント