Python言語とNumPyで配列を扱う際の基礎的な部分をソースコード付きで解説します。
「NumPy」とは?
NumPy(読み:ナムパイ、ナンパイ)は、Pythonで高速かつ効率的に数値計算を行うための基盤ライブラリです。科学技術計算、データ解析、機械学習など、幅広い分野で標準的に利用されています。
| 主な特徴 | 説明 |
|---|---|
| 高速な数値計算 | NumPyは内部処理がC言語やFortranで実装されており、Pythonのリストを使った計算よりも圧倒的に高速です。特に、大規模データや繰り返し計算でその性能差が顕著に現れます。 |
| 多次元配列オブジェクト(ndarray) | NumPyの中心となるデータ構造で、固定長・固定型の配列を効率的に扱えます。メモリ配置が連続しているため、C言語の配列に近い高速なアクセスが可能です。 |
| 豊富な数学関数 | 基本的な算術演算から、線形代数、統計処理、フーリエ変換など、科学計算に必要な関数が幅広く揃っています。 |
| 柔軟なインデックス操作とスライシング | 配列の一部を取り出したり、形状を変えたりする操作が簡潔に書けます。複雑なデータ操作も直感的に記述できます。 |
| 他のライブラリとの強力な連携 | Pandas、SciPy、Matplotlib、scikit-learn、OpenCVなど、多くの科学計算・データ解析ライブラリがNumPyを基盤として動作します。そのため、NumPyの理解はPythonでのデータ分析全般に重要となります。 ・PandasのDataFrameは内部でNumPy配列を利用 ・SciPyはNumPyの機能を拡張する形で構築 |
| ブロードキャスティング(形状の自動拡張) | 異なる形状の配列同士でも、NumPyが自動的に形状を合わせて演算を行います。ループを書かずに高速なベクトル化処理が可能です。 |
動画で見る
本ページの内容は、以下動画で解説しています。
「リスト」ではダメなのか?
Pythonには、C言語の配列に類似する機能として 「リスト」 が標準で備わっています。リストは 要素数を自由に増減できる うえに、異なるデータ型の値を同時に格納できる という柔軟さが特徴です。その一方で、この柔軟性ゆえに 処理速度が遅い という欠点があります。
特に画像処理や機械学習のように、膨大なデータを高速に処理する必要がある分野では、この遅さが大きなボトルネックになります。
そこで登場するのが、Pythonで数値計算を行う際の定番ライブラリである NumPy です。NumPy が提供する ndarray(多次元配列) は、内部処理が C言語や Fortran で実装 されているため、Python のリストと比べて 圧倒的に高速 に動作します。
さらに、NumPy 配列は算術演算子をそのまま使って ベクトル演算や行列演算を直感的に記述できる ため、短いコードで効率的な数値計算を実現できます。高速性と表現力の両方を兼ね備えている点が、NumPy が科学技術計算で広く利用されている理由です。
実行速度の検証
「Pythonリスト」と 「NumPy配列」で同じ処理を行ったとき、どれだけ速度に差が出るのかを比較してみます。以下のコードは、1,000万個の整数データもつ「Pythonリスト」と「NumPy配列」を生成し、1000 万件のデータ(0〜999万の整数を順番に格納した配列)に対して、オイラーの公式$ e^{ix} = \cos(x) + i\sin(x) $で計算を行い、どれだけ処理時間が変わるかを測定しています。
import time
import math
import numpy as np
# 処理する要素数(ここでは 1,000万)
N = 10000000
# 1. Pythonリストでの処理
# 0〜N-1 の整数を順番に格納した Python のリストを作成
lst = list(range(N))
start = time.time() # 計測開始
# リスト内包表記で1つずつ処理
lst_result = [
math.exp(0.000001 * x) * math.sin(x * 0.01) / (1 + (x % 20))
for x in lst
]
end = time.time() # 計測終了
print(f"Pythonリストの処理時間: {end - start:.4f} 秒")
# 2. NumPy配列での処理
# 0〜N-1 の整数を連続したメモリ領域に格納したNumPy配列を生成
arr = np.arange(N)
start = time.time() # 計測開始
# NumPyの関数で一括で計算
arr_result = np.exp(0.000001 * arr) * np.sin(arr * 0.01) / (1 + (arr % 20))
end = time.time() # 計測終了
print(f"NumPy配列の処理時間: {end - start:.4f} 秒")
上記コードをは以下の通りです。
NumPyの処理時間: 0.4213 秒
※実行環境は、Surface Pro 12インチ(メモリ容量:16GB、CPU:Snapdragon X Plus)、Python 3.13.6、NumPy2.3.5
実行結果より、「Pythonリスト」よりも「NumPy配列」のほうが約13.5倍速いことがわかります。
PythonリストとNumPy配列(ndarray)のポイントをまとめると以下のとおりです。
| ポイント | Pythonリスト | NumPy配列(ndarray) |
|---|---|---|
| 処理速度 | 遅い(Pythonレベルのループ) | 大量データ処理で非常に速い(C/Fortran実装) |
| メモリ効率 | 低い(オブジェクト参照の集合) | 高い(連続領域に生データを格納するため大規模データでも省メモリ) |
| データ型 | バラバラでOK | 全要素が同じ dtype |
| ベクトル・行列演算 | for 文が必要 | a + b のように一行で可能。コードが短く、可読性が高い |
なお、本ページ中に何度も登場する「配列」という言葉は「NumPyの配列」を示すものとします。
NumPyのインストール
ターミナル上で、以下のpipコマンドを実行するとインストールできます。
pip install numpy

配列の生成
NumPy では、numpy.array(list, dtype) 関数に Python リストを渡す ことで配列(ndarray)を生成できます。 1次元配列を作る場合は 1 次元リスト、2 次元配列を作る場合は 2 次元リストを渡します。配列のデータ型は dtype 引数で指定します。dtype を省略すると自動的に推定されますが、意図しない型になることがあるため、明示的に指定するほうが安全です。
配列の要素を確認したい場合は、リストと同様に print 関数を使います。
サンプルコード
以下は、配列の生成と中身の確認を行うサンプルコードです。
import numpy as np
# 1次元配列の生成(5日分の株価データ)
prices = np.array([100, 102, 101, 105, 110], dtype='int32')
print(prices.dtype) # int32
print(prices) # [100 102 101 105 110]
# 2次元配列の生成(2銘柄 × 3日分の株価データ)
# 行:銘柄A・銘柄B
# 列:1日目・2日目・3日目
prices_2d = np.array([[100, 102, 101], # 銘柄A
[ 98, 103, 99]], # 銘柄B
dtype='float32')
print(prices_2d.dtype) # float32
print(prices_2d)
# [[100. 102. 101.]
# [ 98. 103. 99.]]
主なデータ型と用途
dtype 引数で指定できる主なデータ型は以下のとおりです。
| 種類 | 説明 | 主な用途 |
|---|---|---|
| bool | 論理値型 | 真偽値の判定、マスク処理 |
| int_ | OS 依存の整数型(64bit OS なら 64bit) | 一般的な整数計算(特に型を気にしない場合) |
| int8 | 8 ビット整数 | メモリ節約が必要な大量データ、軽量な整数処理 |
| int16 | 16 ビット整数 | センサー値、軽量な数値データ |
| int32 | 32 ビット整数 | 一般的な整数計算(標準的な精度) |
| int64 | 64 ビット整数 | 高精度の整数計算、大きな値を扱う場合 |
| uint8 | 8 ビット符号なし整数 | 画像処理(RGB画像は通常 uint8) |
| uint16 | 16 ビット符号なし整数 | 高ダイナミックレンジ画像、センサー値 |
| uint32 | 32 ビット符号なし整数 | 大きな正の整数を扱う場合 |
| uint64 | 64 ビット符号なし整数 | かなり大きな正の整数を扱う場合 |
| float16 | 16 ビット浮動小数点 | メモリ節約、軽量な機械学習モデル |
| float32 | 32 ビット浮動小数点 | 機械学習・深層学習の標準的な実数型 |
| float64 | 64 ビット浮動小数点 | 科学計算・統計解析など高精度が必要な場合 |
| complex64 | 64 ビット複素数 | 信号処理、フーリエ変換(軽量版) |
| complex128 | 128 ビット複素数 | 高精度の複素数計算、科学技術計算 |
初期化不要なら numpy.empty が高速
要素の値を初期化する必要がない場合は、numpy.empty(shape, dtype) を使うと 高速に配列を生成 できます。この場合、引数にはリストではなく 配列の形状(タプル) を指定します。
import numpy as np
# 2 × 3 の空配列を生成(初期化されていないため中身は不定)
prices = np.empty((2, 3), dtype='float32')
print(prices)
# 例:
# [[0. 0. 0. ]
# [0. 0. 0.06643876]]
empty は初期化を行わないため、メモリ上の「ゴミ値」がそのまま入っています。特定の値が必要な場合は zeros() や ones() など、配列を生成するための便利な関数が多数用意されています。
| 関数 | 説明 | 主な用途 |
|---|---|---|
np.zeros(shape, dtype) |
すべて 0 の配列を生成 | 初期化、重みの初期値、空間の確保 |
np.ones(shape, dtype) |
すべて 1 の配列を生成 | バイアス項、テスト用データ |
np.arange(start, stop, step) |
等差数列を生成 | ループ用の数列、インデックス生成 |
np.linspace(start, stop, num) |
指定区間を等分した数列を生成 | グラフ描画の軸、連続値のサンプル生成 |
np.eye(N) |
N×N の単位行列を生成 | 線形代数、行列計算の基礎 |
np.random.rand() |
0〜1 の乱数配列を生成 | 乱数データ、初期値、シミュレーション |
用途に応じて使い分けることで、効率よく配列を作成できます。

配列の四則演算(算術演算子)
NumPy では、算術演算子を使って 配列の要素同士をそのまま四則演算できます。
算術演算子「+」「-」で 2 つのベクトル・行列の加減算が可能です。
ただし、* は 内積ではなく要素ごとの積 になる点に注意しましょう。
内積を計算したい場合は ndarray1.dot(ndarray2) を使います。
以下コードは、株価データを例にした四則演算の使用例です。
import numpy as np
# 3日分の株価データ(例)
prices1 = np.array([100, 102, 101]) # 銘柄A
prices2 = np.array([98, 103, 99]) # 銘柄B
# 加算(2銘柄の株価を単純合計)
print(prices1 + prices2) # [198 205 200]
# 減算(株価差)
print(prices1 - prices2) # [ 2 -1 2]
# 乗算(要素ごとの積:ポートフォリオ比率計算などで利用)
print(prices1 * prices2) # [9800 10506 9999]
# 除算(株価比:相対的な強さの比較)
print(prices1 / prices2) # [1.02040816 0.99029126 1.02020202]
# 剰余(あまり:整数データの処理で利用)
print(prices1 % prices2) # [2 102 2]
# 冪乗(例:株価の2乗)
print(prices1 ** 2) # [10000 10404 10201]
# 符号反転
print(-prices1) # [-100 -102 -101]
要素へのアクセス
配列は、リストと同じように ndarray[index] で要素へアクセス できます。index は 0 始まりで、ndarray[0] は先頭要素、ndarray[1] はその次の要素を示します。
また、負の index を指定すると末尾からアクセスできます(ndarray[-1] は末尾要素)。
スライス(ndarray[i:j])を使えば、i 番目から j−1 番目までの範囲をまとめて取得できます。
以下のコードは、株価の時系列データを1次元配列に格納してアクセスする例です。
import numpy as np
# 5日分の株価データ(例)
price = np.array([100, 102, 101, 105, 110])
# 先頭日の株価
print(price[0]) # 100
# 最終日の株価
print(price[-1]) # 110
# スライスで参照(2~4日目の株価)
print(price[1:4]) # [102 101 105]
# 3日目の株価を修正
price[2] = 999
print(price) # [100 102 999 105 110]
# 2~4日目の株価を一括で書き換え
price[1:4] = [200, 201, 202]
print(price) # [100 200 201 202 110]
2次元配列では、行・列の順に index を指定します。ndarray[i, j] で「i 行目・j 列目」の要素を参照できます。コロン(:)を使うと、行または列を丸ごと取得できます。以下のコードは、株価の時系列データを2次元配列に格納してアクセスする例です。
import numpy as np
# 2銘柄 × 3日分の株価データ
# 行:銘柄A・銘柄B
# 列:1日目・2日目・3日目
prices = np.array([[100, 102, 101], # 銘柄A
[ 98, 103, 99]]) # 銘柄B
# 銘柄Aの2日目の株価(行0, 列1)
print(prices[0, 1]) # 102
# 銘柄Aの全日データ
print(prices[0, :]) # [100 102 101]
# 3日目(列2)の全銘柄の株価
print(prices[:, 2]) # [101 99]
# スライスで参照(銘柄A〜B、2〜3日目)
print(prices[0:2, 1:3])
# [[102 101]
# [103 99]]
# 銘柄Aの3日目の株価を修正
prices[0, 2] = 999
print(prices)
# [[100 102 999]
# [ 98 103 99]]
# 銘柄Bの1〜2日目の株価を一括で書き換え
prices[1, 0:2] = [200, 201]
print(prices)
# [[100 102 999]
# [200 201 99]]
上記コードでは、2次元配列の構成は以下のようになっています。
- 行:銘柄A・銘柄B
- 列:1日目・2日目・3日目
ブールインデックス
ブールインデックスは、True / False の配列(マスク)を使って、条件に合う要素だけを取り出したり、変更したりする NumPy の機能です。
つまり、配列と同じ形の True/False 配列を与えることで、条件に合う要素だけを抽出するマスク処理が簡単に行えます。
以下のコードは、ブールインデックスを用いて要素を取り出したり、書き換える例です。
import numpy as np
# 5日分の株価データ(例)
prices = np.array([100, 102, 98, 105, 110])
# マスク用の配列を生成(True の日だけ抽出)
mask = np.array([True, False, False, True, False])
# True の要素のみ取り出し
selected = prices[mask]
print(selected) # [100 105]
# True の要素のみ値を代入(例:特定日の株価を補正)
prices[mask] = 999
print(prices) # [999 102 98 999 110]
prices[mask]→ True の日の株価だけ取り出すprices[mask] = 999→ True の日の株価だけ書き換える
for文で要素へアクセス
リストと同様に配列でも for 文を使って順に要素へアクセスできます。以下は、for 文で 1 日ずつ株価を取り出す例です。
import numpy as np
# 5日分の株価データ
prices = np.array([100, 102, 101, 105, 110])
# for文 + enumerate でインデックスと値を同時に取得
for day, price in enumerate(prices):
print(f"prices[{day}] = {price}")
# prices[0] = 100
# prices[1] = 102
# prices[2] = 101
# prices[3] = 105
# prices[4] = 110
enumerate() を使うと、インデックス(day)と値(price)を同時に取り出せます。ただし、配列を for 文で 1 要素ずつ処理すると非常に遅くなります。 特に株価分析のような数万〜数百万件の時系列データを扱う場合、for 文は致命的です。可能な限り NumPy の関数や演算子で配列全体を一括処理する のが鉄則です。
良いコード
import numpy as np
prices = np.array([100, 102, 101, 105, 110])
# 100円以上の日のインデックスを取得
index = np.where(prices >= 100)
print("100円以上の日:", index[0]) # [0 1 2 3 4]
NumPy の where() 関数を使うと、条件に合うインデックスを一括で高速に取得できます。
良くないコード
import numpy as np
prices = np.array([100, 102, 101, 105, 110])
# for文で100円以上の日を探索
for i, p in enumerate(prices):
if p >= 100:
print("100円以上の日:", i)
動作は同じですが、データが大きくなると遅くなります。
統計処理
NumPy には、平均値・中央値・分散・標準偏差といった基本的な統計処理から、フーリエ変換のような高度な処理まで、多数の関数が用意されています。以下は、5 日分の株価データに対して、平均値や標準偏差などの統計量を計算する例です。
import numpy as np
# 5日分の株価データ(例)
prices = np.array([100, 102, 101, 105, 110])
# 平均値
avg = np.average(prices)
print("平均値:", avg) # 平均値: 103.6
# 中央値
median = np.median(prices)
print("中央値:", median) # 中央値: 102.0
# 分散(値の散らばり)
var = np.var(prices)
print("分散:", var) # 分散: 13.039999999999997
# 標準偏差(変動の大きさ)
std = np.std(prices)
print("標準偏差:", std) # 標準偏差: 3.6110940170535573
- 平均 → 平均株価
- 中央値 → 典型的な株価
- 分散・標準偏差 → ボラティリティ(変動の大きさ)
- 最大値・最小値 → 最高値・最安値
NumPy で統計量を計算するのによく用いる関数は以下のとおりです。
| 関数 | 内容 |
|---|---|
np.average(x) |
平均値 |
np.mean(x) |
平均値(average と同じ) |
np.median(x) |
中央値 |
np.var(x) |
分散 |
np.std(x) |
標準偏差 |
np.max(x) |
最大値 |
np.min(x) |
最小値 |
np.sum(x) |
合計 |
np.cumsum(x) |
累積和 |

CSVファイルの読み書き
NumPy では、外部ファイルからデータを読み込んで配列に変換するnumpy.genfromtxt(path, delimiter, dtype, skip_header) 関数 が用意されています。
- path:読み込むファイルパス
- delimiter:区切り文字(CSVなら
,) - dtype:データ型(省略すると自動判定)
- skip_header:読み取りをスキップする先頭行数(多くのCSVファイルは1行目がヘッダー行なので、読み飛ばすことが多い)
CSVファイルのようなテキストデータを 1行で配列に変換できる ため、とても便利な関数です。
以下では、株価データが記録されたCSVファイルを読み込む例です。
import numpy as np
# CSVファイルを読み込み(区切り文字はカンマ)
prices = np.genfromtxt('C:/github/sample/python/numpy/fast-tutorial/data.csv', delimiter=',')
# 配列の中身を確認
print(prices)
# [[ 1. 2. 3. 4.]
# [ 5. 6. 7. 8.]
# [ 9. 10. 11. 12.]]
■data.csv
1,2,3,4
5,6,7,8
9,10,11,12
配列を外部ファイルに保存する場合は numpy.savetxt(path, array, delimiter, fmt) 関数 を使います。
- path:保存先ファイルパス
- array:保存する 配列
- delimiter:区切り文字
- fmt:書き込む値のフォーマット(
%dなら整数)
CSV 形式で保存すれば、Excel など多くのソフトで開くことができます。
import numpy as np
# 2次元配列の生成
prices = np.array([[1, 2, 3],
[4, 5, 6]])
# 二乗の計算(例:データ加工)
new_prices = prices ** 2
# CSVファイルに2次元配列のデータを出力
np.savetxt('C:/github/sample/python/numpy/fast-tutorial/new_data.csv', new_prices, delimiter=",", fmt='%d')
■new_data.csv(出力結果)
1,4,9
16,25,36
「Matplotlib」による可視化
Matplotlib(マットプロットリブ) は、Python で最も広く使われている データ可視化ライブラリです。折れ線グラフ、棒グラフ、散布図、ヒストグラムなど、科学技術計算や金融データ分析で必要なほぼすべてのグラフを描画できます。Matplotlibでグラフを描画するplot() 関数などは配列をそのまま引数にできるように作られているため、NumPyとの相性が良いです。
ターミナル上で、以下のpipコマンドを実行するとMatplotlibをインストールできます。
pip install matplotlib
ここでは例として、NumPy を使って 仮想の株価データ(100 日分) を生成し、折れ線グラフとしてMatplotlibで可視化してみます。
import numpy as np
import matplotlib.pyplot as plt
# 乱数の種を固定(毎回同じ結果にするため)
np.random.seed(0)
# 100日分の仮想株価を生成(ランダムウォーク)
days = np.arange(100)
price_changes = np.random.normal(loc=0, scale=1, size=100) # 日ごとの変動
prices = 100 + np.cumsum(price_changes) # 初期値100から積み上げ
# グラフ描画
plt.figure(figsize=(10, 5)) # 描画領域(Figure)を作成し、サイズを指定
plt.plot(days, prices, label="Stock Price", color="blue") # 日数と株価を折れ線グラフとして描画
plt.title("Virtual Stock Price (Random Walk)") # グラフのタイトルを設定
plt.xlabel("Days") # x軸ラベルを設定
plt.ylabel("Price") # y軸ラベルを設定
plt.grid(True) # グリッド線を表示
plt.legend() # 凡例(labelで指定した名前)を表示
plt.show() # グラフを画面に表示
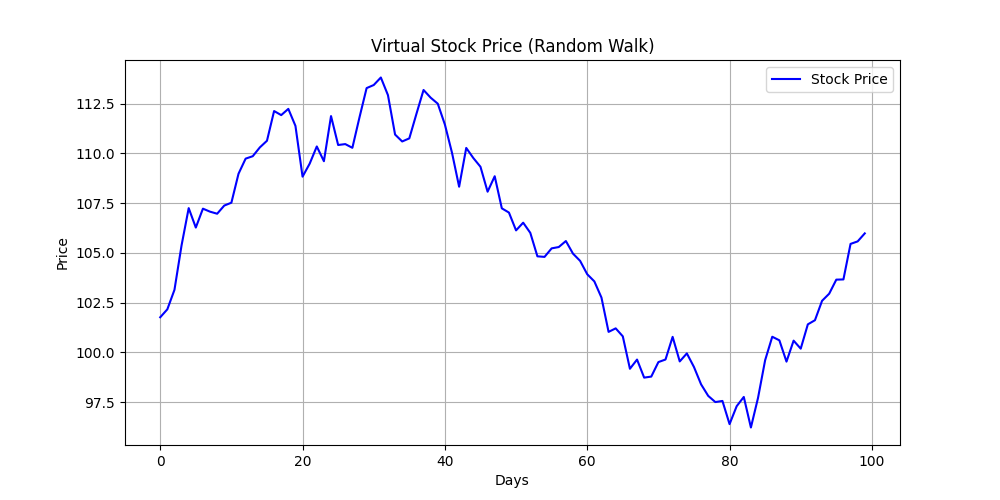
株価はランダムに上下しながら推移することが多いため、NumPy のnp.random.normal() 関数で日ごとの変動を乱数を使って再現しています。 初期値 100 からスタートして、loc=0 は平均 0 、 scale=1 は標準偏差 1、つまり「1日あたり ±1 程度のランダムな変動」を表現しています。np.cumsum() で累積和を取ることで、日々の変動を積み上げて「株価の推移」らしい形にしています。そして、Matplotlibのplt.plot() 関数に配列をそのまま渡して100日間の仮想株価を折れ線グラフとして描画しています。また、タイトルやラベル、凡例の設定なども調整しています。
このように、NumPy と Matplotlib を組み合わて使うことで、大量のデータを計算して可視化する処理をわずか数十行のコードで一気に行うことができます。Matplotlibの基礎については、以下ページでも詳しく解説していますので、興味のある方はこちらもご覧ください。

「Pandas」による時系列データの分析
Pandas(パンダス)は、Excelのような表形式データを扱うためのライブラリで、金融データなどの時系列データの分析でよく使われます。 DataFrame と呼ばれる表形式のデータ構造を中心に操作するため、列名でアクセスできたり、日付をインデックスにしたりと、NumPy よりも直感的に扱えるのが特徴です。
以下のような、ある銘柄のDate(日付)、Open(始値)、Close(終値)の表形式データがあるとします。
| Date | Open | Close |
|---|---|---|
| 2024-01-01 | 2000.5 | 2001.3 |
| 2024-01-02 | 2003.2 | 1999.8 |
| 2024-01-03 | 1998.7 | 2005.4 |
これをPandasの DataFrame で表現すると次のようになります。
import pandas as pd # Pandas を読み込む
# 辞書(dict)形式でサンプルデータを作成
# 3日分の金価格(Open と Close)を用意
data = {
"Date": ["2024-01-01", "2024-01-02", "2024-01-03"], # 日付
"Open": [2000.5, 2003.2, 1998.7], # 始値
"Close": [2001.3, 1999.8, 2005.4], # 終値
}
# 辞書データを DataFrame(表形式データ)に変換
df = pd.DataFrame(data)
# DataFrame の内容を表示
print(df)
# Date Open Close
# 0 2024-01-01 2000.5 2001.3
# 1 2024-01-02 2003.2 1999.8
# 2 2024-01-03 1998.7 2005.4
このように、行 × 列の表形式でデータを扱えるのが Pandas の DataFrame です。Pandasをインストールするには、以下のpip コマンド を実行するだけです。
pip install pandas
Pandasには、DataFrame を効率よく分析するための便利な機能が多数備わっています。ここでは一例として、金価格(XAUUSD)の時系列データを読み込み、直近1年分のデータを抽出して分析・可視化してみます。
import pandas as pd
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
# Stooq が提供しているゴールド価格(XAUUSD)のCSVデータを読み込む
# ゴールド価格の過去から現在までの終値や始値が日ごとに記録されている
url = "https://stooq.com/q/d/l/?s=xauusd&i=d"
df = pd.read_csv(url)
# "Date" 列を文字列(str)から日付(datetime)型に変換する
# こうすることで、「日付として」並べ替えたり、期間で絞り込んだりできるようになる
df["Date"] = pd.to_datetime(df["Date"])
# 日付が古い順(昇順)になるように並べ替える
# Stooq のデータは新しい日付が上に来るため、このままだとグラフが逆向きになってしまう
df = df.sort_values("Date")
# 今日から1年前の日付を計算する
# timedelta(days=365) は「365日前」を表すオブジェクト
one_year_ago = datetime.now() - timedelta(days=365)
# データフレームから「直近1年分だけ」を取り出す
# 条件式 df["Date"] >= one_year_ago を満たす行だけを残している
df_recent = df[df["Date"] >= one_year_ago]
# 1. 基本統計量の表示
# 「Close(終値)」列について、平均・標準偏差・最小値・最大値などの基本統計量を計算
# これにより、「この1年でどのくらいの価格帯で動いていたのか」がざっくり把握できる
print("▼ 直近1年の基本統計量")
print(df_recent["Close"].describe())
# 2. 年初来リターン(最初の終値 → 最新の終値)
# 直近1年のうち、最初の日の終値(スタートの価格)を取り出す
start_price = df_recent["Close"].iloc[0]
# 直近1年のうち、最後の日の終値(最新の価格)を取り出す
end_price = df_recent["Close"].iloc[-1]
# リターン(変化率)を計算する
# (最新価格 - 最初の価格) ÷ 最初の価格 × 100(%表示のため)
return_rate = (end_price - start_price) / start_price * 100
print("\n▼ 年初来リターン")
print(f"{return_rate:.2f}%") # 小数点以下2桁まで表示
# 3. 移動平均線(SMA)を追加
# 「20日移動平均」を直近20日間の終値の平均を1日ずつずらしながら計算
df_recent["SMA_20"] = df_recent["Close"].rolling(window=20).mean() # 20日移動平均
# 「60日移動平均」を計算する(より長い期間のトレンドを見る指標)
df_recent["SMA_60"] = df_recent["Close"].rolling(window=60).mean() # 60日移動平均
# 4. ボリンジャーバンド(Bollinger Bands)を追加
# 20日の標準偏差
df_recent["STD_20"] = df_recent["Close"].rolling(window=20).std()
# ボリンジャーバンド(±2σ)
df_recent["BB_upper"] = df_recent["SMA_20"] + 2 * df_recent["STD_20"]
df_recent["BB_lower"] = df_recent["SMA_20"] - 2 * df_recent["STD_20"]
# 5. グラフ描画
# グラフ全体のサイズを指定(横12インチ × 縦5インチ)
plt.figure(figsize=(12, 5))
# 終値の折れ線グラフを描画(横軸に日付、縦軸に終値Closeを使う)
plt.plot(df_recent["Date"], df_recent["Close"], label="Close", color="gold")
# 20日移動平均線を青色で描画
plt.plot(df_recent["Date"], df_recent["SMA_20"], label="SMA 20", color="blue", alpha=0.7)
# 60日移動平均線を赤色で描画
plt.plot(df_recent["Date"], df_recent["SMA_60"], label="SMA 60", color="red", alpha=0.7)
# ボリンジャーバンド(上限・下限)
plt.plot(df_recent["Date"], df_recent["BB_upper"], label="BB Upper", color="green", alpha=0.5)
plt.plot(df_recent["Date"], df_recent["BB_lower"], label="BB Lower", color="green", alpha=0.5)
# バンドの塗りつぶし(視覚的にわかりやすくなる)
plt.fill_between(df_recent["Date"], df_recent["BB_upper"], df_recent["BB_lower"],
color="green", alpha=0.1)
plt.title("Gold Price Trend (Stooq XAUUSD) - Last 1 Year") # グラフのタイトル
plt.xlabel("Date") # 横軸(x軸)のラベル
plt.ylabel("Price (USD)") # 縦軸(y軸)のラベル
plt.grid(True) # 背景にグリッド(目盛りの補助線)を表示
plt.legend() # 凡例
plt.show() # グラフを画面に表示
count 258.000000
mean 3357.093217
std 466.031196
min 2585.340000
25% 2983.687500
50% 3334.725000
75% 3643.315000
max 4356.070000
Name: Close, dtype: float64
▼ 年初来リターン
57.16%
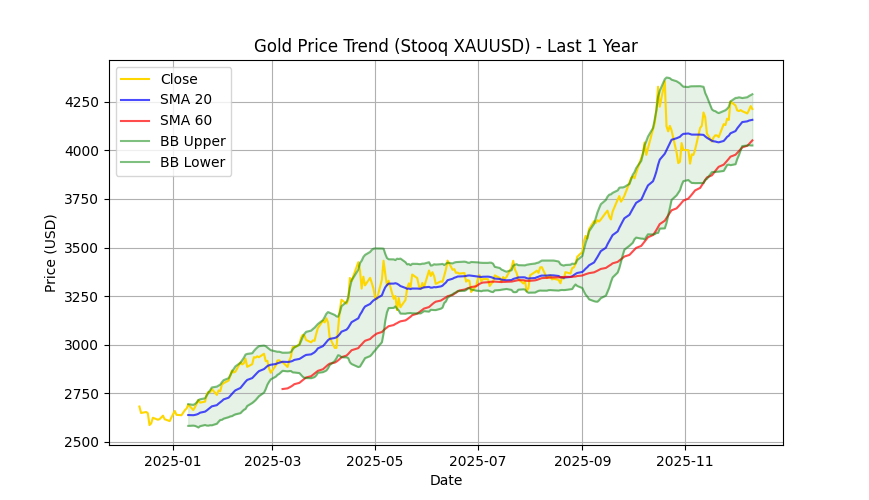
移動平均線は、価格の流れ(トレンド)をなめらかにして見るための指標です。短期と長期の移動平均を比べることで、相場の方向性をつかみやすくなります。一般的には、短期の移動平均が長期の移動平均を上抜くと上昇トレンドに入りやすい、逆に下抜くと下落トレンドに入りやすいと考えられます。一方、ボリンジャーバンドは、移動平均線の上下に「±2σ(標準偏差)」の幅を持たせたバンドで、価格の「行き過ぎ」や「変動の大きさ」を判断するために使われます。価格が 上限バンド付近にあると買われすぎ(上がりすぎ)、下限バンド付近にあると売られすぎ(下がりすぎ) の可能性があると考えられます。また、バンドが広がっているときは相場が大きく動いている状態、狭まっているときは値動きが落ち着いている状態を示します。
Pandas と Matplotlib を組み合わて使うことで、このような時系列データの読み込み → 整形 → 分析 → 可視化 までを、わずか数十行のコードで一気に行うことができます。Pandasの基礎については、以下ページでも詳しく解説していますので、興味のある方はこちらもご覧ください。

関連コンテンツ
NumPyの様々な使い方については、以下ページにまとめていますので、ご活用ください。



コメント