Python言語とNumPyを用いて、高速逆フーリエ変換とローパス処理を行い、ノイズを取り除く方法をソースコード付きで解説します。
【正弦波の場合】FFTとローパスフィルタでノイズ除去
Python + NumPyでフーリエ変換によるローパスフィルタ処理(高周波ノイズ除去)を実装してみます。
まず、周期信号(振幅1・周波数5Hzと振幅0.2・40Hzの正弦波を重ね合わせたもの)を入力し、高周波成分(振幅0.2・40Hzの正弦波)を削ってみます。
今回実装したプログラムの処理手順は以下の通りです。
| – | 処理手順 |
|---|---|
| ① | 時間信号(周波数5の正弦波 + 周波数40の正弦波)を生成します。 |
| ② | 高速フーリエ変換により、時間信号を周波数信号に変換します。 |
| ③ | カットオフ周波数fcを超える帯域の周波数信号の値を0にします。 |
| ④ | 高速逆フーリエ変換により、周波数信号を時間信号に変換します。 |
| ⑤ | 処理結果をグラフに表示します。 |
ソースコード
サンプルプログラムのソースコードです。
実行結果
サンプルプログラム実行結果です。
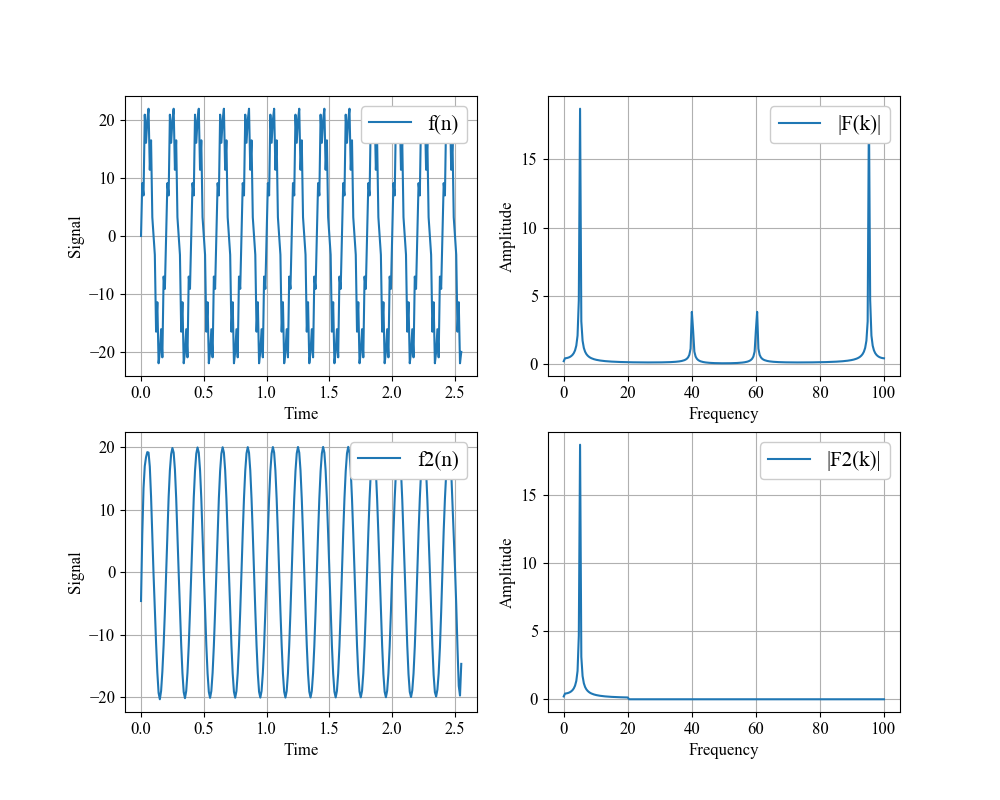
上が「処理前の時間信号・周波数信号」、下が「処理後の時間信号・周波数信号」です。
カットオフ周波数20でローパスフィルタ処理しているので、高周波成分(周波数40の正弦波)がうまく除去できていることがわかります。
【矩形波の場合①】FFTとローパスフィルタでノイズ除去
続いて、周波数5Hzの矩形波に対して、カットオフ周波数20Hzでローパスフィルタをかけてみます。
ソースコード
サンプルプログラムのソースコードです。
実行結果
サンプルプログラム実行結果です。
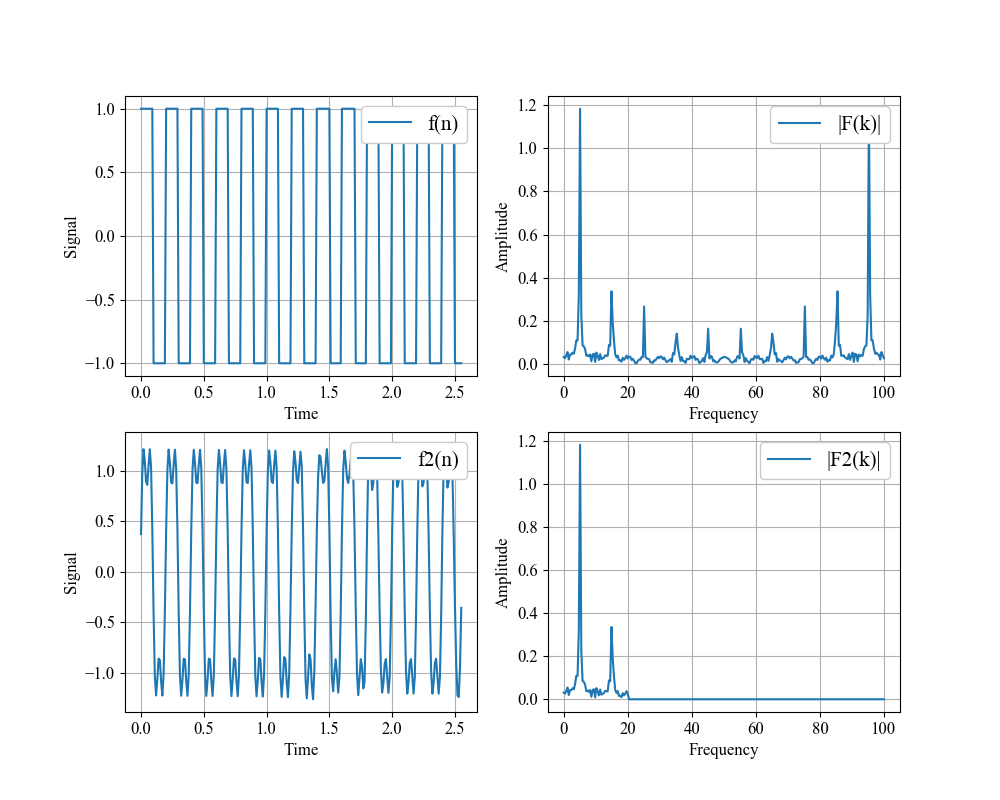
カットオフ周波数20でローパスフィルタ処理しているのに、周波数5Hzの矩形波の情報が一部欠落しています。
これは、低周波の矩形波はフーリエ変換で周波数空間に変換される際、」低周波の正弦波 + 高周波の正弦波の重ね合わせ」で近似的に表現されるためです。
そのため、周波数空間上でローパスフィルタにより高周波成分をカットすると、「高周波の正弦波分」が削除され、高速逆フーリエ変換で時間空間に戻したときに一部欠落したような形になります。
そのため、矩形波の信号を扱う場合は注意が必要です。
【矩形波の場合②】FFTとローパスフィルタでノイズ除去
周波数5Hzと20Hzの矩形波を重ね合わせた入力信号に対して、カットオフ周波数10Hzでローパスフィルタをかけてみます。
ソースコード
サンプルプログラムのソースコードです。
実行結果
サンプルプログラム実行結果です。
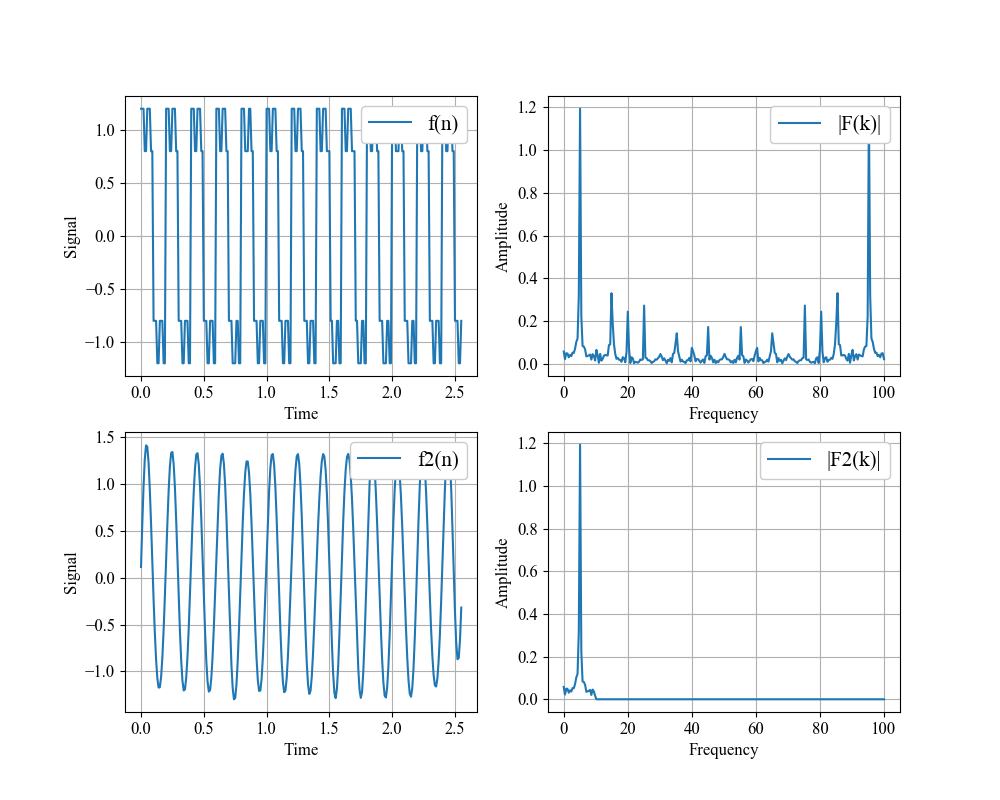
先程も説明したとおり、高周波の矩形波成分だけでなく、低周波の矩形波成分の一部も欠落します。
【非周期信号の場合】FFTとローパスフィルタでノイズ除去
非周期信号(振幅1・周波数5Hzと振幅0.2・40Hzの正弦波を重ね合わせ、大半を0にしたもの)を入力し、カットオフ周波数20Hzでローパスフィルタをかけてみます。
ソースコード
サンプルプログラムのソースコードです。
実行結果
サンプルプログラム実行結果です。
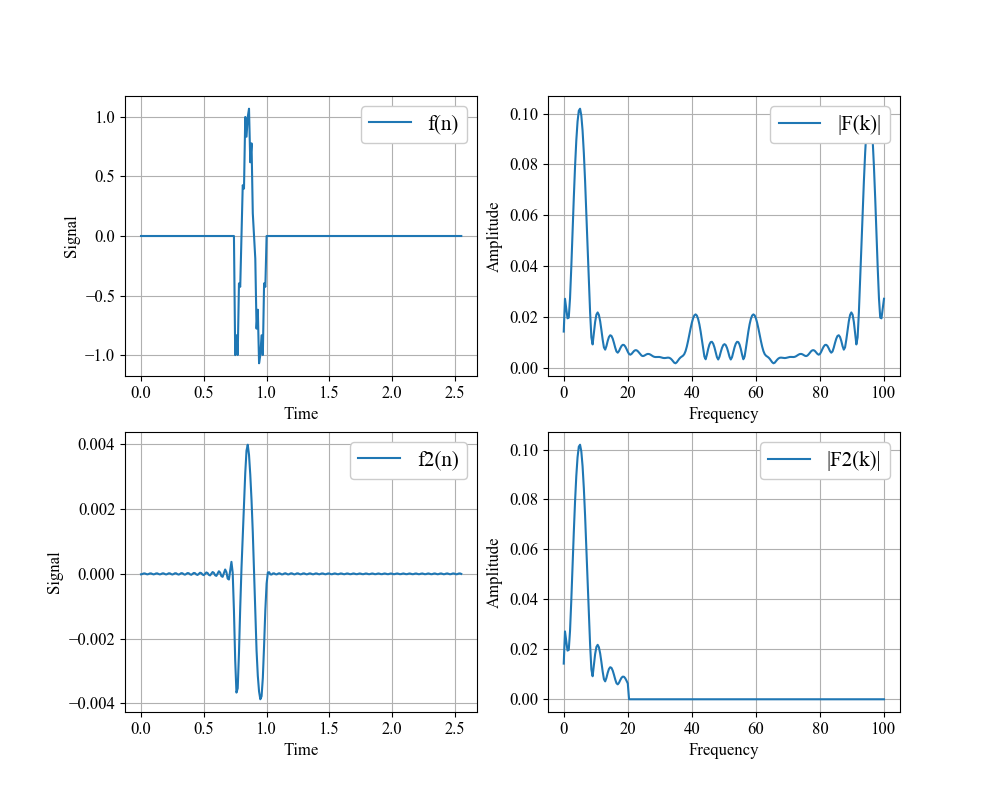
周期信号と比べて高周波成分が残っており、精度が悪くなっています。


コメント