【NumPy】高速フーリエ変換 （FFT）で振幅スペクトルを計算

Python言語とNumPyを用いて、信号データを高速フーリエ変換(FFT)して周波数スペクトルを求める方法をソースコード付きで解説します。

【Python】高速フーリエ変換

高速フーリエ変換（Fast Fourier Transform:FFT）とは、フーリエ変換を高速化したものです。
フーリエ変換とは、デジタル信号を周波数解析するのに用いる処理です。
PythonモジュールNumpyでは「numpy.fft.fft」を用いることで高速フーリエ変換を実装できます。

404 NOT FOUND | Python入門速報

python.joho.info

メソッド

サンプルプログラムのソースコードです。

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt


# データのパラメータ
N = 256            # サンプル数
dt = 0.01          # サンプリング間隔
f1, f2 = 10, 20    # 周波数
t = np.arange(0, N*dt, dt) # 時間軸
freq = np.linspace(0, 1.0/dt, N) # 周波数軸

# 信号を生成（周波数10の正弦波+周波数20の正弦波+ランダムノイズ）
f = np.sin(2*np.pi*f1*t) + np.sin(2*np.pi*f2*t) + 0.3 * np.random.randn(N)

# 高速フーリエ変換
F = np.fft.fft(f)

# 振幅スペクトルを計算
Amp = np.abs(F)

# グラフ表示
plt.figure()
plt.rcParams['font.family'] = 'Times New Roman'
plt.rcParams['font.size'] = 17
plt.subplot(121)
plt.plot(t, f, label='f(n)')
plt.xlabel("Time", fontsize=20)
plt.ylabel("Signal", fontsize=20)
plt.grid()
leg = plt.legend(loc=1, fontsize=25)
leg.get_frame().set_alpha(1)
plt.subplot(122)
plt.plot(freq, Amp, label='|F(k)|')
plt.xlabel('Frequency', fontsize=20)
plt.ylabel('Amplitude', fontsize=20)
plt.grid()
leg = plt.legend(loc=1, fontsize=25)
leg.get_frame().set_alpha(1)
plt.show()

実行結果

サンプルプログラム実行結果です。
■入力信号（左）と振幅スペクトル（右）

振幅スペクトルを見ると、低周波側（10, 20Hz）のスペクトルが大きいことがわかります。
これは、入力信号が2つの正弦波（周波数10と20）の合成波であるためです。

サンプリング間隔が0.01なのでサンプリング周波数は100Hzとなります。
高周波側(80, 90Hz)のスペクトルは、0Hz～50Hzの正の周波数(sin)に対して、-50Hz～0Hzの負の周波数(cos)に相当する成分です。
入力信号が実数の場合、低周波側と高周波側のスペクトルは対称になりますが、複素数の場合は非対称になります。

【NumPy】高速フーリエ変換でパワースペクトル解析

Python言語とNumPyを用いて、高速フーリエ変換(FFT)でパワースペクトルを計算する方法をソースコード付きで解説します。

python.joho.info

2017.03.20

【FFT応用】ローパスフィルタでノイズ除去

Python + NumPyでフーリエ変換によるローパスフィルタ処理（高周波ノイズ除去）を実装してみます。
まず、周期信号(振幅1・周波数5Hzと振幅0.2・40Hzの正弦波を重ね合わせたもの）を入力し、高周波成分（振幅0.2・40Hzの正弦波）を削ってみます。

今回実装したプログラムの処理手順は以下の通りです。

ソースコード

サンプルプログラムのソースコードです。

実行結果

サンプルプログラム実行結果です。

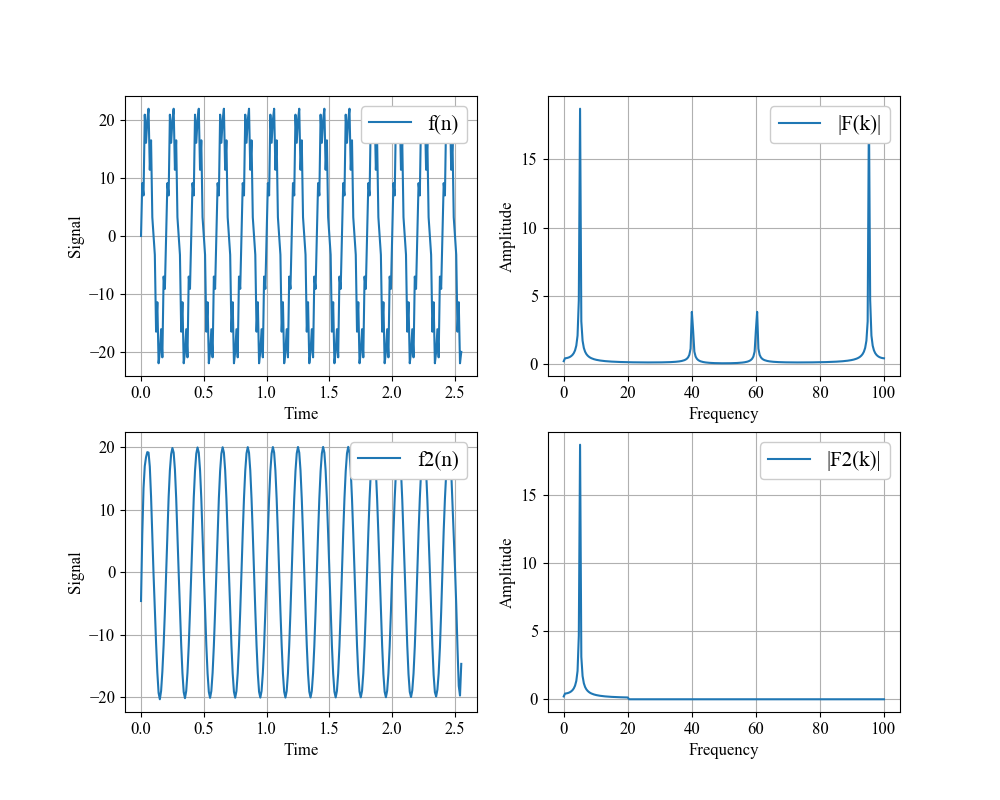
上が「処理前の時間信号・周波数信号」、下が「処理後の時間信号・周波数信号」です。
カットオフ周波数20でローパスフィルタ処理しているので、高周波成分（周波数40の正弦波）がうまく除去できていることがわかります。

【NumPy】高速フーリエ変換とローパスフィルタでノイズ除去

Python言語とNumPyを用いて、高速逆フーリエ変換とローパス処理を行い、ノイズを取り除く方法をソースコード付きで解説します。

python.joho.info

2020.01.20

【FFT応用】ハイパスフィルタでノイズ除去

Python + NumPyでフーリエ変換によるハイパスフィルタ処理（高周波ノイズ抽出）を実装してみます。
今回実装したプログラムの処理手順は以下の通りです。

サンプルプログラムのソースコードです。

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt


def main():
    # データのパラメータ
    N = 256            # サンプル数
    dt = 0.01          # サンプリング間隔
    fq1, fq2 = 5, 40    # 周波数
    fc = 20            # カットオフ周波数
    t = np.arange(0, N*dt, dt) # 時間軸
    freq = np.linspace(0, 1.0/dt, N) # 周波数軸

    # 時間信号（周波数5の正弦波 + 周波数40の正弦波）の生成
    f = np.sin(2*np.pi*fq1*t) + 0.5 * np.sin(2*np.pi*fq2*t)

    # 高速フーリエ変換（周波数信号に変換）
    F = np.fft.fft(f)

    # 正規化 + 交流成分2倍
    F = F/(N/2)
    F[0] = F[0]/2

    # 配列Fをコピー
    F2 = F.copy()

    # ハイパス処理（カットオフ周波数未満の帯域と、右半分の帯域の周波数信号を0にする）
    F2[(freq < fc)] = 0
    F2[(freq > 1/(dt*2))] = 0

    # 高速逆フーリエ変換（時間信号に戻す）
    f2 = np.fft.ifft(F2)

    # 振幅を元のスケールに戻す
    f2 = np.real(f2*N)

    # グラフ表示
    plt.figure()
    plt.rcParams['font.family'] = 'Times New Roman'
    plt.rcParams['font.size'] = 17

    # 時間信号（元）
    plt.subplot(221)
    plt.plot(t, f, label='f(n)')
    plt.xlabel("Time", fontsize=20)
    plt.ylabel("Signal", fontsize=20)
    plt.grid()
    leg = plt.legend(loc=1, fontsize=25)
    leg.get_frame().set_alpha(1)

    # 周波数信号(元)
    plt.subplot(222)
    plt.plot(freq, np.abs(F), label='|F(k)|')
    plt.xlabel('Frequency', fontsize=20)
    plt.ylabel('Amplitude', fontsize=20)
    plt.grid()
    leg = plt.legend(loc=1, fontsize=25)
    leg.get_frame().set_alpha(1)

    # 時間信号(ハイパス処理後)
    plt.subplot(223)
    plt.plot(t, f2, label='f2(n)')
    plt.xlabel("Time", fontsize=20)
    plt.ylabel("Signal", fontsize=20)
    plt.grid()
    leg = plt.legend(loc=1, fontsize=25)
    leg.get_frame().set_alpha(1)

    # 周波数信号(ハイパス処理後)
    plt.subplot(224)
    plt.plot(freq, np.abs(F2), label='|F2(k)|')
    plt.xlabel('Frequency', fontsize=20)
    plt.ylabel('Amplitude', fontsize=20)
    plt.grid()
    leg = plt.legend(loc=1, fontsize=25)
    leg.get_frame().set_alpha(1)
    plt.show()


if __name__ == "__main__":
    main()

実行結果

サンプルプログラム実行結果です。

上が「処理前の時間信号・周波数信号」、下が「処理後の時間信号・周波数信号」です。
カットオフ周波数20でハイパスフィルタ処理しているので、高周波成分（周波数40の正弦波）がうまく抽出できていることがわかります。

【NumPy】フーリエ変換とハイパスフィルタでノイズ抽出

Python言語とNumPyを用いて、高速逆フーリエ変換とローパス処理を行い、ノイズを取り出す方法をソースコード付きで解説します。

python.joho.info

2018.01.17