Python版OpenCVの「cv2.Canny()関数」でCannyアルゴリズムを実装し、輪郭検出する方法をソースコード付きで解説します。
Cannyアルゴリズムとは
Canny法は、画像の輪郭(エッジ)部分を検出するアルゴリズムです。このアルゴリズムを実装した輪郭検出器は「Cannyエッジ検出器」などと呼ばれています。
輪郭を検出する他のアルゴリズムとしては「ソーベルフィルタ」「ラプラシアンフィルタ」など有名ですが、それらと比較して細かい輪郭を検出でき、ノイズにも強いという優れた特徴があります。
以下の画像は、Cannyアルゴリズムで輪郭検出した結果です。
■入力画像(左)、出力画像(右)


「Cannyアルゴリズム」「ソーベルフィルタ」「ラプラシアンフィルタ」で作成した輪郭画像を目の部分を拡大して見比べると以下のようになります。
■Cannyアルゴリズム(左)、ラプラシアンフィルタ(中央)、ソーベルフィルタ(右)



ラプラシアンフィルタはノイズに弱いため、ごま塩ノイズが目立ちます。
Sobelフィルタはごま塩ノイズは見られないものの、細かい輪郭は検出できていないことがわかります。
Cannyアルゴリズムはごま塩ノイズが見られず、細かい輪郭も検出できていることがわかります。
ただし、次節で解説するように、Cannyアルゴリズムは複数のステップを踏んで処理を行うため計算コストが高く、パラメータの調整が必要という欠点もあります。
Cannyアルゴリズムの原理や仕組みについては以下ページで別途解説しています。

今回は、以下の2通りの方法で処理を実装する方法を解説します。
① OpenCVの「cv2.Canny()関数」で簡単に実装(1行で書けて処理速度も速い)
② 自分でアルゴリズムを書いて実装(Cannyアルゴリズムの仕組みを理解するため、2重forループでNumPy配列にアクセスしているため、処理速度はかなり遅い)
解説動画
サンプルコード① cv2.Cannyで実装
以下は、cv2.Cannyで実装した場合のサンプルプログラムのソースコードです。
実行結果
サンプルプログラムの実行結果です。
■入力画像(左)と出力画像(右)


コード解説
「cv2.Canny()関数」の使い方は以下のとおりです。
dst = cv2.Canny(src, threshold1, threshold2[, apertureSize[, L2gradient]])
| パラメータ名 | 説明 |
|---|---|
| src | 入力画像 |
| threshold1 | 最小閾値(Hysteresis Thresholding処理で使用)。この値が低いほど、より多くの輪郭が検出されますが、ノイズも増えます。 |
| threshold2 | 最大閾値(Hysteresis Thresholding処理で使用)。この値が高いほど、より信頼性の高い輪郭だけが検出されます。 |
| apertureSize | 微分画像を求めるのに使用されるSobelフィルタのカーネルサイズ。(例:3, 5, 7)。 |
| L2gradient | 勾配の大きさを求める方法。デフォルト値はFalseで、L1ノルム(X方向の絶対値とY方向の絶対値の和)を使用します。Trueのときは、L2ノルム(X方向の2乗とY方向の2乗の和の平方根)を用います。 |
サンプルコード② トラックバーでパラメータ調整
以下は、cv2.Canny()関数のパラメータをトラックバーで調整できるようにした場合のサンプルプログラムのソースコードです。
実行結果
サンプルプログラムの実行結果です。
最小閾値と最大閾値を低くすると、以下のようにノイズが多くなります。
■入力画像(左)と出力画面(右)

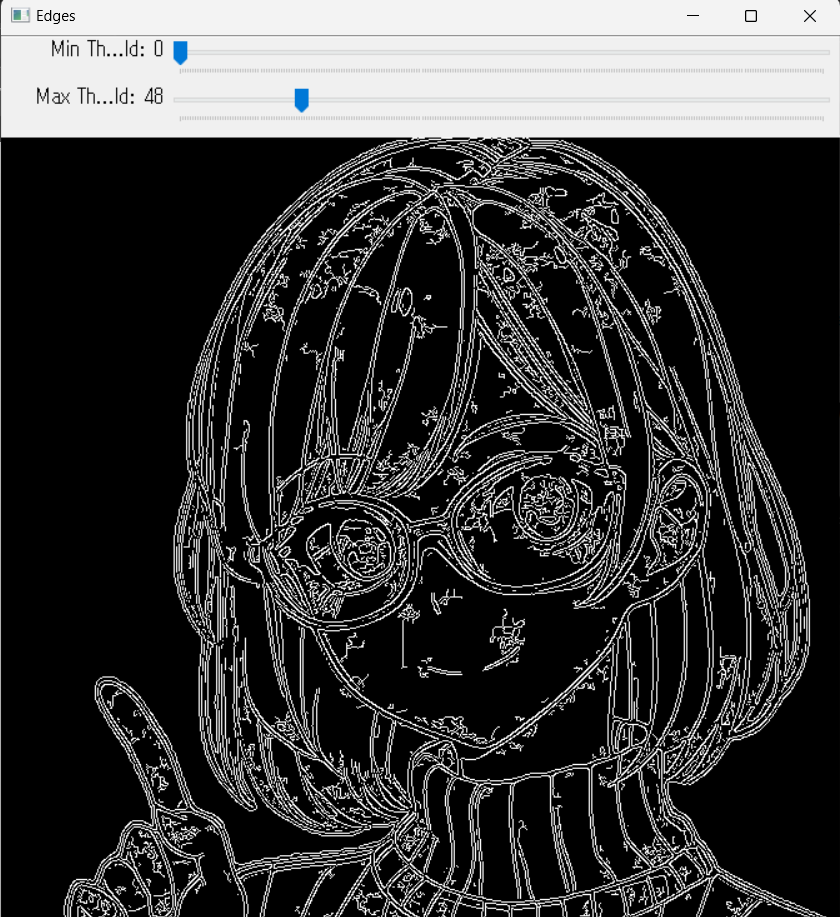
コード解説
Min ThresholdとMax Thresholdという名前のトラックバーを2つウィンドウEdgesに作成します。値の初期値はそれぞれ50と100、最大値は2つとも255に設定します。
また、トラックバーの値が変更されるとupdate_edges関数が呼び出されます。
# トラックバーの作成
cv.createTrackbar('Min Threshold', 'Edges', 50, 255, update_edges)
cv.createTrackbar('Max Threshold', 'Edges', 100, 255, update_edges)
- `cv.createTrackbar('Min Threshold', 'Edges', 50, 255, update_edges)`:
- `cv.createTrackbar('Max Threshold', 'Edges', 100, 255, update_edges)`: という名前のトラックバーをウィンドウ`Edges`に作成し、最大閾値の初期値を100に設定します。トラックバーの値が変更されると`update_edges`関数が呼び出されます。
- ウィンドウが最初に表示されたときに、初期エッジ画像を表示するために
update_edges関数を一度呼び出します。
# 初期エッジ画像の表示 update_edges(0)
- 以下の
update_edges関数は、ウィンドウが最初に表示された時とトラックバーの値が変更されたときに呼び出されます。トラックバーから最小閾値と最大閾値を取得し、Cannyアルゴリズムで輪郭を検出します。
# 輪郭検出を更新する関数
def update_edges(val):
# トラックバーの現在の最小閾値を取得
min_thresh = cv.getTrackbarPos('Min Threshold', 'Edges')
# トラックバーの現在の最大閾値を取得
max_thresh = cv.getTrackbarPos('Max Threshold', 'Edges')
# Cannyアルゴリズムの適用
edges = cv.Canny(gray, min_thresh, max_thresh)
# 輪郭画像の表示
cv.imshow('Edges', edges)
サンプルコード③ 自分でアルゴリズムを書いて実装
以下は、自分でアルゴリズムを書いて実装した場合のサンプルプログラムのソースコードです。
コード解説
コードのポイントを解説します。なお、畳み込み演算を定義しているfilter2d関数については、以下ページで別途解説していますので、ここでは解説を省略します。

- 以下の「canny_edge_detecter」関数では、Cannyアルゴリズムの全体的な処理をまとめています。
def canny_edge_detecter(gray, t_min, t_max, d):
# 処理1 ガウシアンフィルタで平滑化
kernel_g = np.array([[1/16, 1/8, 1/16],
[1/8, 1/4, 1/8],
[1/16, 1/8, 1/16]])
# ガウシアンフィルタ
G = filter2d(gray, kernel_g, -1)
# 処理2 微分画像の作成(Sobelフィルタ)
kernel_sx = np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
kernel_sy = np.array([[-1, -2, -1],
[0, 0, 0],
[1, 2, 1]])
Gx = filter2d(G, kernel_sx, 0)
Gy = filter2d(G, kernel_sy, 0)
# 処理3 勾配強度・方向を算出
G = np.sqrt(Gx**2 + Gy**2)
Gth = np.arctan2(Gy, Gx) * 180 / np.pi
# 処理4 Non maximum Suppression処理
G = non_max_sup(G, Gth)
# 処理5 Hysteresis Threshold処理
return hysteresis_threshold(G, t_min, t_max, d)
- 以下の「Non maximum Suppression」関数では、勾配方向に基づき、注目画素とその周囲の画素を比較して、注目画素が最大値でない場合、画素値を0に修正します。
つまり、信頼性の低い輪郭を除去しています。
# Non maximum Suppression処理
def non_max_sup(G, Gth):
h, w = G.shape
dst = G.copy()
# 勾配方向を4方向(垂直・水平・斜め右上・斜め左上)に近似
Gth[np.where((Gth >= -22.5) & (Gth < 22.5))] = 0
Gth[np.where((Gth >= 157.5) & (Gth < 180))] = 0
Gth[np.where((Gth >= -180) & (Gth < -157.5))] = 0
Gth[np.where((Gth >= 22.5) & (Gth < 67.5))] = 45
Gth[np.where((Gth >= -157.5) & (Gth < -112.5))] = 45
Gth[np.where((Gth >= 67.5) & (Gth < 112.5))] = 90
Gth[np.where((Gth >= -112.5) & (Gth < -67.5))] = 90
Gth[np.where((Gth >= 112.5) & (Gth < 157.5))] = 135
Gth[np.where((Gth >= -67.5) & (Gth < -22.5))] = 135
# 注目画素と勾配方向に隣接する2つの画素値を比較し、注目画素値が最大でなければ0に
for y in range(1, h - 1):
for x in range(1, w - 1):
if Gth[y][x] == 0:
if (G[y][x] < G[y][x+1]) or (G[y][x] < G[y][x-1]):
dst[y][x] = 0
elif Gth[y][x] == 45:
if (G[y][x] < G[y-1][x+1]) or (G[y][x] < G[y+1][x-1]):
dst[y][x] = 0
elif Gth[y][x] == 90:
if (G[y][x] < G[y+1][x]) or (G[y][x] < G[y-1][x]):
dst[y][x] = 0
else:
if (G[y][x] < G[y+1][x+1]) or (G[y][x] < G[y-1][x-1]):
dst[y][x] = 0
return dst
- 以下の「hysteresis_threshold」関数では、指定された閾値の範囲に基づき、輪郭の強度が閾値未満であれば、信頼性の低いとして除去する処理です。
# hysteresis_threshold処理
def hysteresis_threshold(src, t_min=75, t_max=150, d=1):
h, w = src.shape
dst = src.copy()
for y in range(0, h):
for x in range(0, w):
# 最大閾値より大きければ信頼性の高い輪郭
if src[y][x] >= t_max:
dst[y][x] = 255
# 最小閾値より小さければ信頼性の低い輪郭(除去)
elif src[y][x] < t_min:
dst[y][x] = 0
# 最小閾値~最大閾値の間なら、近傍に信頼性の高い輪郭が1つでもあれば輪郭と判定、無ければ除去
else:
if np.max(src[y-d:y+d+1, x-d:x+d+1]) >= t_max:
dst[y][x] = 255
else:
dst[y][x] = 0
return dst
実行結果
以下の画像は、サンプルプログラムの実行結果です。
■入力画像(左)と出力画像(右)


関連ページ



コメント