Python版OpenCVで画像のテンプレートマッチングを行う方法をソースコード付きで解説します。
テンプレートマッチングとは
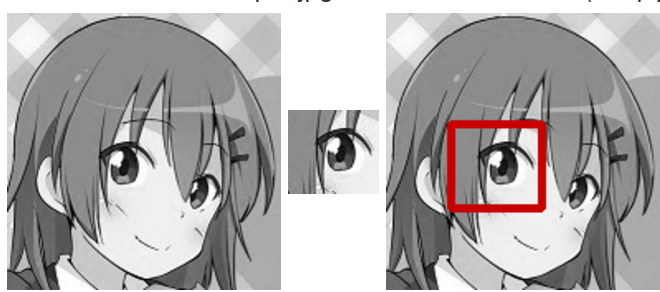
テンプレートマッチング(Template matching)とは、以下のように入力画像中からテンプレート画像と最も類似する箇所を探索する処理です。
■左から順に入力画像、テンプレート画像、出力画像


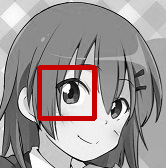
※出力画像の赤枠部分は、テンプレートマッチングによりテンプレート画像と最も類似する部分と判定された箇所です。
※お借りした画像:プロ生ちゃん(暮井 慧)
アルゴリズムの詳細は以下ページで解説しています。

動画解説版
本ページの内容は以下動画でも解説しています。
SSDで実装
SSD(Sum of Squared Difference)では、「画素値の差分の二乗和(二乗誤差)」で類似度を評価します。
この場合、SSDの値が最小になる場所が類似度が最も高いことになります。
入力画像の画素値を$I(x,y)$、テンプレート画像の画素値を$T(x,y)$とします。
また、テンプレート画像の幅を$w$, 高さを$h$とします。
走査位置が$dx,dy$の場合、SSDの値は次式で計算できます。
$ SSD(d_x, d_y)={\displaystyle \sum_{x=0}^{w-1}} {\displaystyle \sum_{y=0}^{h-1}} (I(d_x+x,d_y+y)-T(x,y))^2 $
例えば、テンプレート画像の幅$w=2$、高さ$h=2$のとき、$SSD(1, 0)$の計算式は以下になります。
$ SSD(1, 0)={\displaystyle \sum_{x=0}^{1} \sum_{y=0}^{1}}(I(1+x,y)-T(x,y))^2 $
サンプルコード①
OpenCVの「cv2.matchTemplate()関数」でテンプレートマッチングの処理を実装した場合のサンプルコードです。
サンプルコード①の解説
サンプルコード①のポイントを解説します。
img = cv2.imread("C:/github/sample/python/opencv/template-matching/input.png")
temp = cv2.imread("C:/github/sample/python/opencv/template-matching/temp.png")
- cv2.imread: 指定したパスから画像を読み込みます。
imgは入力画像、tempはテンプレート画像です。
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
temp = cv2.cvtColor(temp, cv2.COLOR_RGB2GRAY)
- cv2.cvtColor: カラー画像をグレースケール画像に変換します。テンプレートマッチングは通常、グレースケール画像で行われます。
h, w = temp.shape
- temp.shape: テンプレート画像の高さ(h)と幅(w)を取得します。
match = cv2.matchTemplate(gray, temp, cv2.TM_SQDIFF)
min_value, max_value, min_pt, max_pt = cv2.minMaxLoc(match)
pt = min_pt
- cv2.matchTemplate: テンプレートマッチングを実行します。
cv2.TM_SQDIFFはマッチング手法に二乗差の総和(SSD)を指定しています。 - cv2.minMaxLoc: マッチング結果の最小値とその位置を取得します。
min_ptはスコアが最小の走査位置(テンプレート画像と最も類似する位置)です。min_valueはスコアが最小のときの類似度(スコア)です。max_ptはスコアが最大の走査位置(テンプレート画像と最も類似しない位置)です。max_valueはスコアが最大のときの類似度(スコア)です。
cv2.rectangle(img, (pt[0], pt[1]), (pt[0] + w, pt[1] + h), (0, 0, 200), 3)
cv2.imwrite("C:/github/sample/python/opencv/template-matching/ssd1.png", img)
- cv2.rectangle: 入力画像上にテンプレート画像が一致した領域を矩形で描画します。
- cv2.imwrite: 結果画像を保存します。
サンプルコード②
OpenCVの「cv2.matchTemplate」は使用せず、NumPyでテンプレートマッチングの処理を実装した場合のサンプルコードです。
サンプルコード②の解説
サンプルコード②のポイントを解説します。
pt = template_matching_ssd(gray, temp)
定義したテンプレートマッチング関数を使用して、テンプレート画像と最も類似する位置を取得します。
テンプレートマッチング関数の中身は以下のとおりです。
def template_matching_ssd(src, temp):
h, w = src.shape
ht, wt = temp.shape
score = np.empty((h-ht, w-wt))
for dy in range(0, h - ht):
for dx in range(0, w - wt):
diff = (src[dy:dy + ht, dx:dx + wt] - temp)**2
score[dy, dx] = diff.sum()
pt = np.unravel_index(score.argmin(), score.shape)
return (pt[1], pt[0])
この関数は、入力画像srcとテンプレート画像tempを受け取り、テンプレート画像と最も類似する位置を返します。
さらに、関数の中身を順に解説します。
h, w = src.shape
ht, wt = temp.shape
入力画像srcとテンプレート画像tempの高さと幅を取得します。
score = np.empty((h-ht, w-wt))
スコアを格納するための二次元配列scoreを作成します。この配列のサイズは、入力画像のサイズからテンプレート画像のサイズを引いたものです。
for dy in range(0, h - ht):
for dx in range(0, w - wt):
入力画像をテンプレート画像のサイズで走査します。
dyとdxはそれぞれ縦方向と横方向の走査位置を示します。
diff = (src[dy:dy + ht, dx:dx + wt] - temp)**2
score[dy, dx] = diff.sum()
現在の走査位置における入力画像の部分領域とテンプレート画像との差を計算し、その二乗誤差の和を求めます。この値をスコア配列に格納します。
pt = np.unravel_index(score.argmin(), score.shape)
スコア配列の中で最小の値を持つ位置を取得します。np.unravel_indexを用いて、一次元配列のインデックスを二次元配列のインデックスに変換します。
return (pt[1], pt[0])
最小スコアの位置を返します。この位置がテンプレート画像と最も類似する部分の位置です。
実行結果
サンプルプログラムの実行結果です。
■左から入力画像(input.jpg)、テンプレート画像(temp.jpg)、出力画像(result.jpg)



SADで実装
SAD(Sum of Absolute Difference)では、「画素値の差分の絶対値の和」で類似度を評価します。
この場合もSADの値が最小になるときが類似度が最も高いことになります。
入力画像の画素値を$I(x,y)$、テンプレート画像の画素値を$T(x,y)$とします。
また、テンプレート画像の幅を$w$, 高さを$h$とします。
走査位置が$dx,dy$の場合、SADの値は次式で計算できます。
$ SAD(d_x, d_y)={\displaystyle \sum_{x=0}^{w-1} \sum_{y=0}^{h-1}}|I(d_x+x,d_y+y)-T(x,y)| $
SADが最小となる走査位置が、テンプレート画像に最も類似する部分の左上座標となります。
SADはSSDと比べて以下の特徴があります。
- 計算量が少ない(メリット)
- 外れ値の影響を受けにくい(メリット)
- 照明の影響をかなり受けやすい(デメリット)※SSDもそれなりに影響を受ける
サンプルコード①
cv2.matchTemplateメソッドでSADを実装したサンプルコードです。
SSDのサンプルコード①との違いは、cv2.matchTemplateメソッドの第三引数に「cv2.TM_SQDIFF_NORMED」を指定している点です。
match = cv2.matchTemplate(gray, temp, cv2.TM_SQDIFF_NORMED)
サンプルコード②
cv2.matchTemplateメソッドを使わずにSADを実装したサンプルコードです。
SSDのサンプルコード②との違いは、テンプレートマッチング関数内で差分の絶対和を計算している点です。
# 差分の絶対和を計算
diff = np.abs(src[dy:dy + ht, dx:dx + wt] - temp)
実行結果
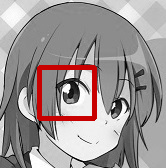
サンプルプログラムの実行結果です。
■左から入力画像(input.jpg)、テンプレート画像(temp.jpg)、出力画像(result.jpg)


NCCで実装
NCC(Normalized Cross Correlation)では、「正規化相互相関」で類似度を評価します。
入力画像の画素値を$I(x,y)$、テンプレート画像の画素値を$T(x,y)$とします。
また、テンプレート画像の幅を$w$, 高さを$h$とします。
走査位置が$dx,dy$の場合、NCCの値は次式で計算できます。
$ NCC(d_x, d_y)=\frac{ \sum \sum [ I(d_x+x,d_y+y)T(x,y)] } { \sqrt{\sum \sum [I(d_x+x,d_y+y)]^2} \sqrt{ \sum \sum [T(x,y)]^2} } $
ここで、
$ \sum \sum = {\displaystyle \sum_{x=0}^{w-1} \sum_{y=0}^{h-1}} $
NCCの値は-1.0~1.0に収まり、最大値1.0に最も近くなった走査位置が、テンプレート画像に最も類似する部分の左上座標となります。
- 照明の影響を受けにくい(メリット)
- 計算量が多い(デメリット)
NCCは、テンプレート画像と入力画像の部分領域の輝度値を正規化します。これにより、画像の相対的な輝度パターンを比較することができます。
また、テンプレート画像と入力画像の部分領域の内積を計算します。内積は、ベクトルの方向を比較するものであり、ベクトルの大きさ(輝度の絶対値)には依存しません。これらの理由により、「照明変化に比較的強い」という利点があります。
サンプルコード①
OpenCVの「cv2.matchTemplate」を使用し、NCCの計算を実装した場合のサンプルコードです。
cv2.matchTemplateメソッドの第三引数に「cv2.TM_CCORR_NORMED」を指定しています。
サンプルコード②
OpenCVの「cv2.matchTemplate」は使用せず、NumPyでNCCの計算を実装した場合のサンプルコードです。
上記コードで、NCCの計算は以下のように行っています。
num = np.sum(roi * temp)
den = np.sqrt((np.sum(roi ** 2))) * np.sqrt(np.sum(temp ** 2))
if den == 0:
score[dy, dx] = 0
score[dy, dx] = num / den
numは窓画像とテンプレート画像の画素値の積の総和です。denは窓画像とテンプレート画像の画素値の二乗和の平方根の積です。denが0の場合、スコアを0に設定します(ゼロ除算を防ぐため)。- 類似度スコアを
num / denとして計算し、スコア配列に格納します。
pt = np.unravel_index(score.argmax(), score.shape)
スコア配列の中で最大の値を持つ位置を取得します。np.unravel_indexを用いて、一次元配列のインデックスを二次元配列のインデックスに変換します。この位置がテンプレート画像と最も類似する部分の位置です。
実行結果
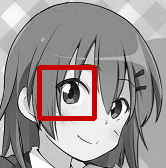
サンプルプログラムの実行結果です。
■左から入力画像(input.jpg)、テンプレート画像(temp.jpg)、出力画像(result.jpg)


ZNCCで実装
ZNCC(Zero means Normalized Cross Correlation)では、「零平均正規化相互相関」と呼ばれる統計量で類似度を評価します。
入力画像の画素値を$I(x,y)$、テンプレート画像の画素値を$T(x,y)$とします。
また、テンプレート画像の幅を$w$, 高さを$h$とします。
走査位置が$dx,dy$の場合、ZNCCの値は次式で計算できます。
$ ZNCC(d_x, d_y)=\frac{ \sum \sum [ (I(d_x+x,d_y+y)-\mu_I)(T(x,y)-\mu_T] } { \sqrt{\sum \sum [I(d_x+x,d_y+y)-\mu_I]^2} \sqrt{ \sum \sum [T(x,y)-\mu_T]^2} } $
ここで、
$ \sum \sum = {\displaystyle \sum_{x=0}^{w-1} \sum_{y=0}^{h-1}} $
$\mu_I, \mu_T$は、入力画像とテンプレート画像の平均値です。
ZNCCの値は-1.0~1.0に収まり、最大値1.0に最も近くなった走査位置が、テンプレート画像に最も類似する部分の左上座標となります。
計算過程で平均値を引くため、比較する2つの画像領域の平均値が異なっていても類似度が変化しません。つまり、NCCよりも明るさの変動に対してよりロバストとなります。
原理の詳細は以下ページで解説しています。
サンプルコード
OpenCVの「cv2.matchTemplate」を使用し、ZNCCの計算を実装した場合のサンプルコードです。
cv2.matchTemplateメソッドの第三引数に「cv2.TM_CCOEFF_NORMED」を指定しています。
実行結果
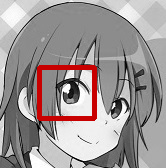
サンプルプログラムの実行結果です。
■左から入力画像(input.jpg)、テンプレート画像(temp.jpg)、出力画像(result.jpg)


関連ページ


コメント