Pythonライブラリ「scikit-learn」で単回帰分析を行う方法についてサンプルコード付きで解説します。
単回帰分析とは
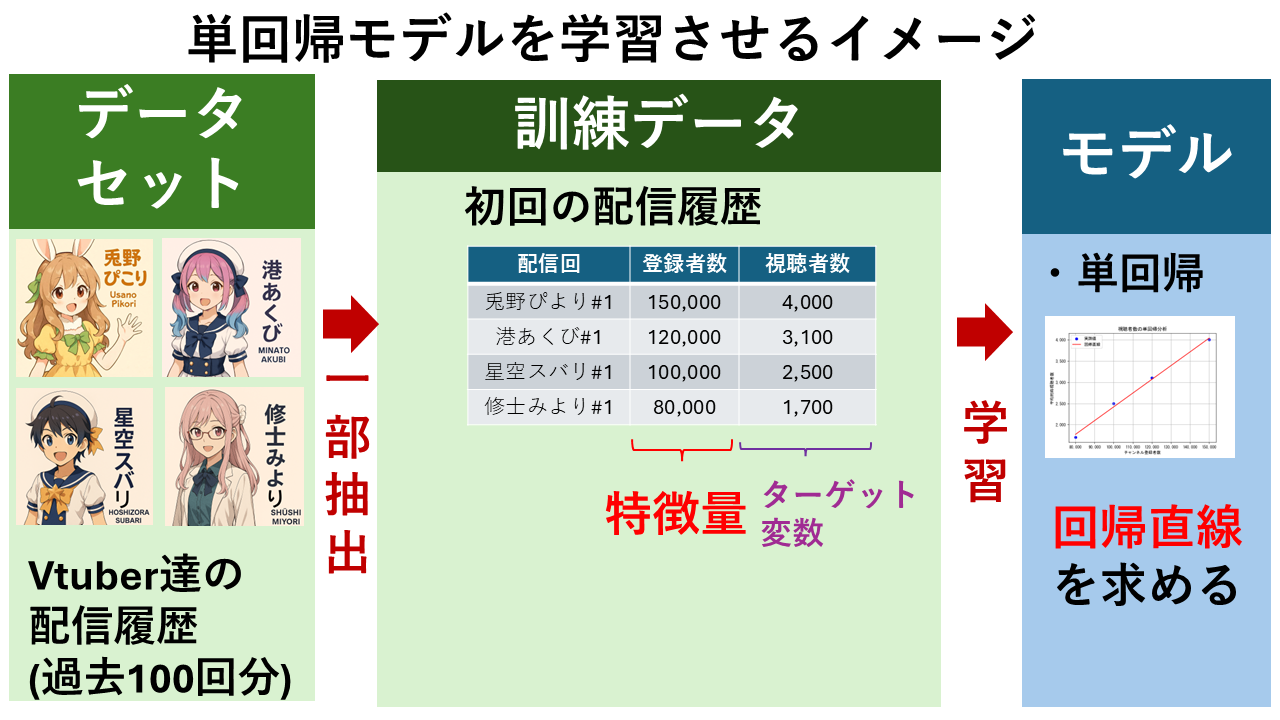
以下の図は、VTuberの「チャンネル登録者数」から「視聴者数」を予測する単回帰モデルを作成するイメージです。
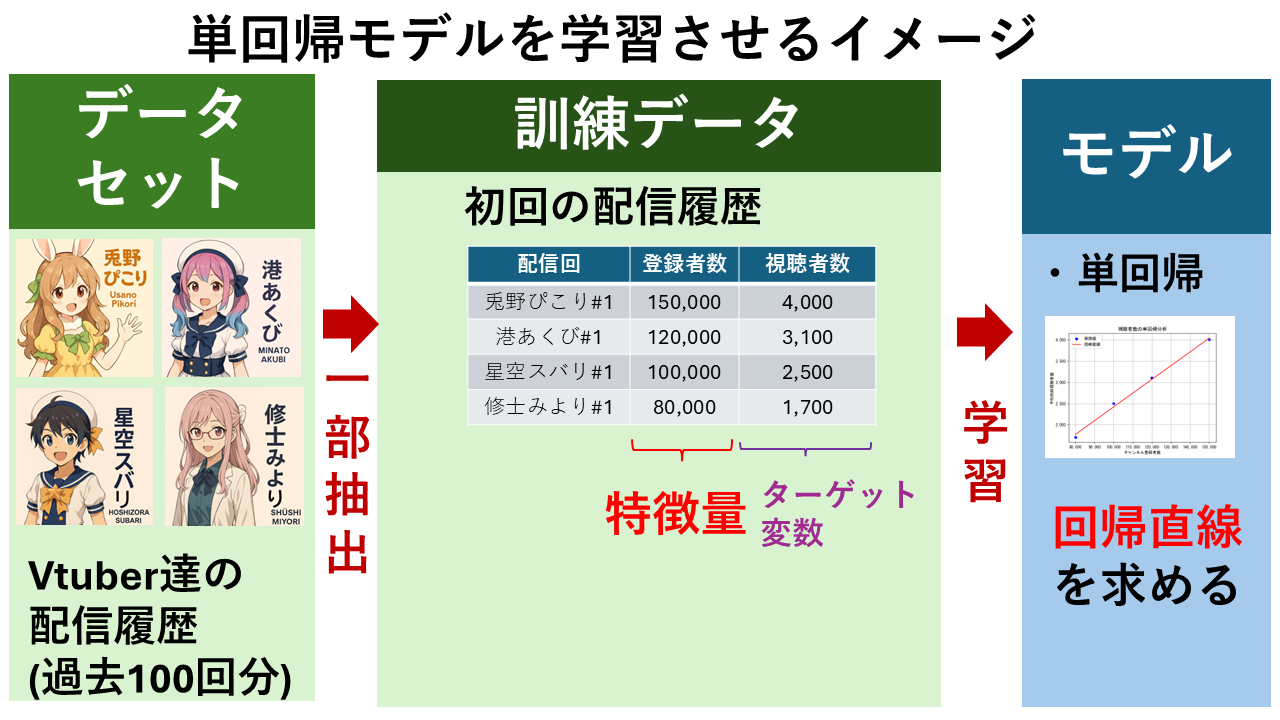
単回帰分析(Simple Linear Regression)では、1つの特徴量($x$)から1つのターゲット変数($y$)を予測するモデルを作成します。数学的には以下の式で表されます。
予測値を計算する式:$ \hat{y} = ax + b $
実測値の関係:$ y = ax + b + \varepsilon $
各変数の意味をまとめると以下表になります。例は、VTuberの「チャンネル登録者数」から「視聴者数」を予測する場合です。
| 変数 | 説明 | 例 |
|---|---|---|
| $ \hat{y} $ | モデルが計算したターゲット変数(目的変数)の推定値 | 視聴者数(予測値) |
| $ y $ | 実際に観測されたターゲット変数(目的変数)の値 | 視聴者数(実測値) |
| $ x $ | 特徴量(予測したい値に影響を与えるもの。説明変数ともいう) | チャンネル登録者数(実測値) |
| $ a $ | 傾き($x$が1増えると$y$がどれだけ増えるか。重み、回帰係数ともいう) | 登録者数が1人増えたときの視聴者数の増加量 |
| $ b $ | 切片($x=0$のときの$y$の値) | 登録者数が0人のときの理論的な視聴者数 |
| $ ε $ | 誤差項(予測と実際のズレ) | 「モデルが説明できない部分」であり、ノイズや他の未考慮の要因を含みます。 |
予測値を計算する式 $ \hat{y} = ax + b $は、「$x$に比例して$\hat{y}$が変化する関係」を表す、傾き$a$、切片$b$の一次関数です。グラフにすると以下のようなまっすぐな直線になります。この直線を「回帰直線」といいます。
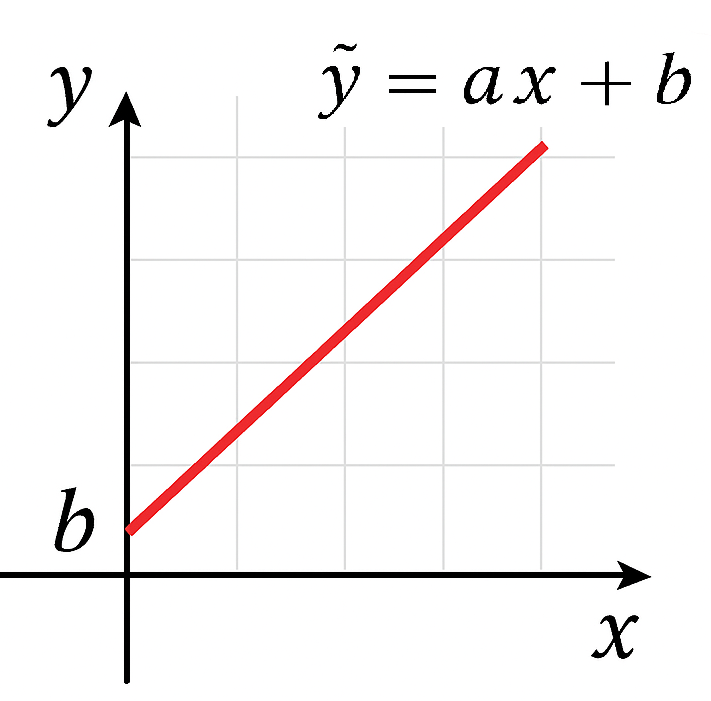
単回帰分析の仕組みについては、以下ページで別途解説しています。
動画で見る
サンプルコード① 単回帰モデルの作成
Pythonライブラリ「Scikit-learn」を用いて、単回帰分析によりVTuberの「チャンネル登録者数」から「視聴者数」を予測してみましょう。

以下のような4名のVTuberの初回配信における「チャンネル登録者数」と「視聴者数」の実測値のデータがあるとします。
| 配信回 | チャンネル登録者数(x) | 視聴者数(y) |
|---|---|---|
| 兎野ぴこり#1 | 150,000 | 4,000 |
| 港あくび#1 | 120,000 | 3,100 |
| 星空スバリ#1 | 100,000 | 2,500 |
| 修士みより#1 | 80,000 | 1,700 |
scikit-learnのLinearRegression クラスを使って、「チャンネル登録者数」から「視聴者数」を予測する回帰直線を求めるPythonプログラムを作成すると、以下のようになります。
切片 b: -823.3644859813076
予測視聴者数: 5662.616822429906
実行結果の解説
小数第4位で切り捨てすると、回帰直線の式は以下のように求まります。
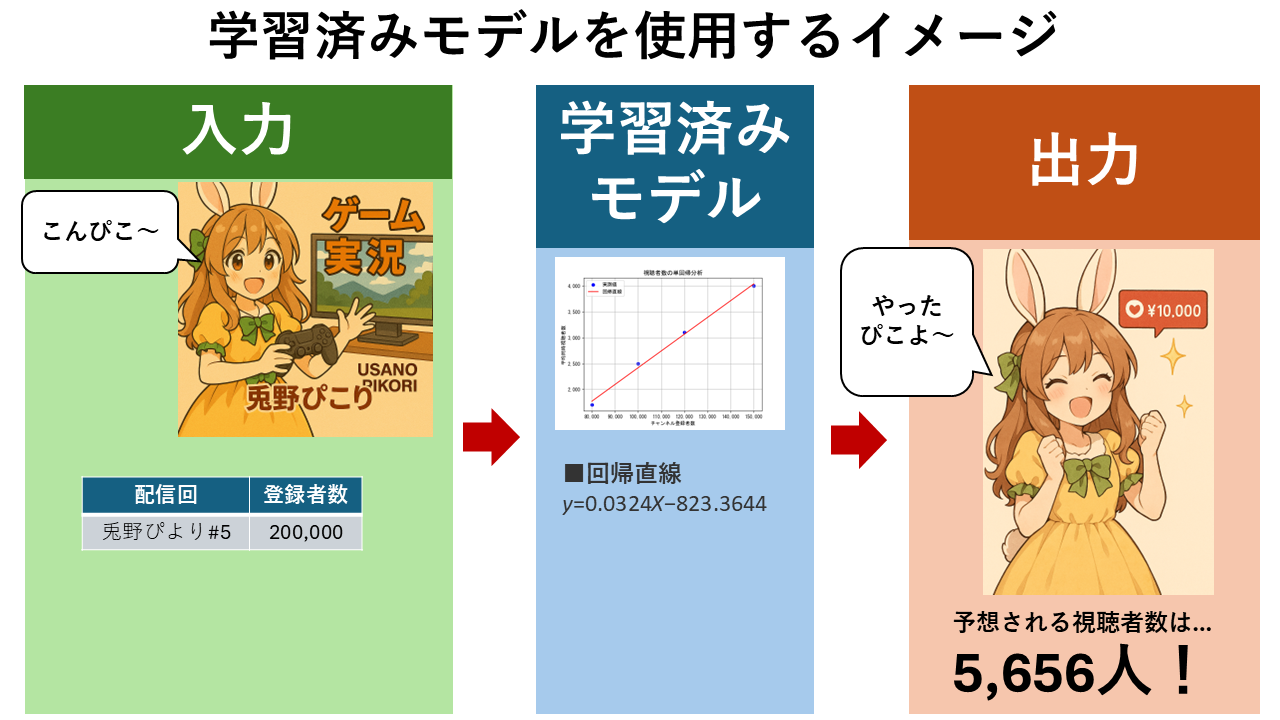
$ \hat{y} = 0.0324x – 823.3644 $
上式の$ \hat{y} $は視聴者数の推測値、$x$はチャンネル登録者数となります。
よって、例えばチャンネル登録者数20万人の視聴者数は以下の計算により、約5656人と推定できます。
$ \hat{y} = 0.0324 \times 200,000 – 823.3644 = 5656.6356$
なお、どのような計算により回帰直線を求めているかなど、数理的な仕組みについては、以下ページで学ぶことができます。
コード解説
from sklearn.linear_model import LinearRegression
import numpy as np
LinearRegressionは、線形回帰モデルを使うためのクラスnumpyは、数値配列を扱うためのライブラリ
# 特徴量(説明変数): VTuberのチャンネル登録者数
X = np.array([[150000], [120000], [100000], [80000]])
# ターゲット変数(目的変数): 視聴者数
y = np.array([4000, 3100, 2500, 1700])
Xは 特徴量(チャンネル登録者数)で、2次元配列(shape = (4, 1))にしているのは、sklearnの仕様に合わせるためです。yは ターゲット変数(視聴者数)で、1次元配列。
# 線形回帰モデルを用いて、登録者数と視聴者数の関係を学習
model = LinearRegression()
model.fit(X, y)
model = LinearRegression()は 線形回帰モデルのクラス(LinearRegression)からインスタンスを生成(model)。model.fit(X, y)で、訓練データ(X:特徴量、y:ターゲット変数)でモデルが学習します。fitメソッドは、最小二乗法で最も誤差が少ない直線を求めています。
# 回帰直線の傾き(登録者数が1人増えるごとの視聴者数の増加量)を出力
print("傾き a:", model.coef_[0])
# 回帰直線の切片(登録者数が0人のときの理論的な視聴者数)を出力
print("切片 b:", model.intercept_)
model.coef_属性(プロパティ)は、学習後に得られる 回帰係数(重み) がNumPy配列で格納されています。model.coef_[0]は単回帰直線の傾き$a$(登録者数が1人増えると、視聴者数がどれだけ増えるか)。- 傾き$a$ ≈ 0.0324 → 登録者数が1万人増えると、視聴者数は約324人増える。
model.intercept_は 学習後に得られる切片$b$が「float型の数値(単回帰)」または「NumPy配列(重回帰)」で格納されています(登録者数が0人だった場合の理論的な視聴者数)。- 切片 ≈ -823 → 実際には「視聴者数がマイナスになる」ということはありえません。これは、モデルがデータの外側まで予測しようとしたために、現実とは合わない結果が出ています。こうした「データの外側での予測」は、正しくないことが多く、これを「外挿の限界」と呼びます。
# チャンネル登録者数20万人のときの視聴者数を予測
new_subscriber = np.array([[200000]])
# 予測された視聴者数を表示
predicted_viewers = model.predict(new_subscriber)
print("予測視聴者数:", predicted_viewers[0])
登録者数が20万人のVTuberに対して、視聴者数を予測。model.predict() に新しいデータを渡すと、学習済みの回帰式を使って予測値を返します。
動画で見る
サンプルコード② 学習済みモデルの保存・読み込み
Scikit-leaenで学習したモデルを保存したり、保存したモデルを読み込んで使用する方法を紹介します。
大量のデータで学習すると時間がかかりますが、一度保存すれば再学習せずにすぐ使えます。また、複数のモデルを保存しておけば、後から別のプロジェクトで使用したり、他のモデルとの性能比較や検証を行うこともできます。
学習済みモデルの保存
以下は、学習済みモデルを「sample02-1.learn」ファイルに保存するプログラムです。
サンプルコード①と異なる点に絞って解説します。
import joblib
joblibは、モデルを保存・読み込みするためのライブラリです。
joblib.dump(model, "C:/github/sample/python/scikit-learn/tutorial/LinearRegression/single/sample02-1.learn")
ここでは学習済みモデルを指定したパスに保存しています。 .learnという拡張子は任意です。後で joblib.load() で読み込めば、再学習せずに予測に使えます。あとは、サンプルコード①と同じ内容です。
学習済みモデルの再利用
以下は、「sample02-1.learn」ファイルを読み込み、学習済みモデルを使ってチャンネル登録者数20万人のときの視聴者数を予測するプログラムです。
サンプルコード①と異なる点に絞って解説します。
# 学習済みモデルの読み込み
model = joblib.load(
"C:/github/sample/python/scikit-learn/tutorial/LinearRegression/sample02-1.learn"
)
ここでは指定したパスの学習済みモデルを読み込んでいます。 sample02-1.learnは先程保存した学習済みモデルです。あとは、サンプルコード①と同じ内容です。

サンプルコード③ CSVファイルを読み込んで学習
CSVファイルは、ExcelやGoogle Sheetsで作成・確認が可能です。既存の業務データはCSV形式でエクスポートすれば、すぐに活用できます。
以下は、CSVファイルを読み込み、訓練データとして単回帰モデルを作成するコードです。
■dataset01.csv(読み込むデータ)
※リンクを右クリックするとダウンロードできます。
コード解説
これまでのサンプルコードとは異なる、重要な箇所に絞って解説します。
import pandas as pd
pandas: データフレーム操作ライブラリをインポートします。CSVの読み込みや列抽出に使用します。
dataset = pd.read_csv(
"C:/github/sample/python/scikit-learn/tutorial/LinearRegression/single/dataset01.csv",
sep=",",
)
- CSVファイルを読み込み、
datasetという名前でPandasのDataFrame に格納しています。 sep=","はCSVファイルの区切り文字にカンマを指定しています。
x = dataset.loc[:, ["チャンネル登録者数"]].to_numpy()
y = dataset["視聴者数"].to_numpy()
dataset.loc[:, ["チャンネル登録者数"]]:全行(:)から「チャンネル登録者数」列だけを抽出。scikit-learn の LinearRegression().fit(x, y) は、xにDataFrame(2次元)を与える必要がある。.to_numpy()によって pandas の Series/DataFrame を NumPy 配列に変換。x: 特徴量(チャンネル登録者数)を2次元配列としてDataFrameから抽出(抽出データは、DataFrame(2次元)形式)。y: ターゲット変数(視聴者数)を1次元配列としてDataFrameから抽出(抽出データは、Series(1次元)形式)。

このように、単回帰モデルの仕組みを理解していなくても、「Scikit-learn」を用いれば簡単にできてしまいます。しかし、作成したモデルの性能を評価したり、改善を行うには仕組みについてもある程度理解する必要があります。以下ページは、これから学びたい人や仕組みの理解について不安のある人向けの解説を行っています。
サンプルコード④ 相関係数
相関係数 $r$ は、2つの変数の関係の強さを表す指標です。単回帰分析では「特徴量」と「ターゲット変数」の関係の強さを確かめることができます。つまり、「そもそも登録者数と視聴者数に関係があるのか?」ということを確認ができます。相関係数 $r$の範囲は −1〜+1 で、以下のように関係性の傾向を知ることができます。
| 相関係数 $r$ | 関係の強さ | 例 |
|---|---|---|
| $r = +1$ | 完全な正の相関 | 登録者数が増えると視聴者数も必ず増える |
| $r \approx +0.8$ | 強い正の相関 | 登録者数が増えると視聴者数も増える傾向がある |
| $r = 0$ | 無相関 | 登録者数と視聴者数に関係がない |
| $r \approx -0.8$ | 強い負の相関 | 登録者数が増えると視聴者数が減る傾向がある |
| $r = -1$ | 完全な負の相関 | 登録者数が増えると視聴者数が必ず減る |
相関係数の計算方法など、数理的な内容は以下ページで解説しています。
サンプルコード③に相関係数を求める機能を追加したものが以下になります。
※読み込んだデータ:dataset01.csv
「相関係数 r: 0.9887097324786042」となり、特徴量(登録者数)とターゲット変数(視聴者数)の間に、高い相関性がある(ほぼ線形の関係性がある)ことがわかります。単回帰モデルの前提(線形性)がかなり妥当である可能性が高いです。ただし、これは相関の強さであって、因果関係を示すものではありません。「強い相関=良いモデル」ではないので、注意が必要です。良いモデルかどうかを判断するには、次に解説する「汎化性能の検証」などを行います。
コード解説
これまでのサンプルコードとは異なる、重要な箇所に絞って解説します。
# 相関係数を算出
correlation = np.corrcoef(dataset["チャンネル登録者数"], dataset["視聴者数"])[0, 1]
print("相関係数 r:", correlation)
dataset["チャンネル登録者数"]は、特徴量(説明変数)。Pandas Series(1次元配列)形式。dataset["視聴者数"]は、ターゲット変数(目的変数)。Pandas Series(1次元配列)形式。np.corrcoef(x, y)は、2つの配列の相関係数行列を返すNumPyの関数です。[0, 1]は、相関係数行列の中から、xとyの相関係数だけを抽出しています。

サンプルコード⑤ 訓練用データに対する適合性
訓練データに対する適合性評価は、学習済みモデルが訓練用データにどれだけ合っているかを決定係数 $ R^2 $などの指標で評価することです。ただし、スコアが高すぎると、過学習の可能性もあるので注意が必要です。
決定係数 $ R^2 $ は、回帰直線が実測値(訓練用データなど)にどれだけうまく沿っているかを示す指標です。決定係数$ R^2 $は 0〜1の範囲の値をとります。値が1に近いほど、実測値に近いと評価できます。
- $ R^2 = 1 $:すべての実測値が回帰直線上にあり、完全に再現できている。(理想的なモデル)
- $ R^2 \approx 0.8 $:実測値が回帰直線の付近にあり、高い予測精度がある。(実用的なモデル)
- $ R^2 = 0 $:実測値が回帰直線から大きく外れており、予測精度が低い。(不適なモデル)
決定係数の計算方法など、数理的な内容は以下ページで解説しています。

サンプルコード④に、決定係数を求める機能を追加したものが以下になります。
※読み込んだデータ:dataset01.csv
コード解説
これまでのサンプルコードとは異なる、重要な箇所に絞って解説します。
from sklearn.metrics import r2_score
scikit-learnのmetricsモジュールには、モデルの性能を評価する関数が多数あります。r2_scoreはその中の1つで、回帰モデルの決定係数(R²)を計算する関数です。
r2_train = r2_score(y_train, y_train_pred)
r2_score()は、実際の値y_trainと予測値y_train_predの一致度を評価し、訓練データに対する決定係数 R² が得られます。
print("訓練データに対する R²(決定係数):", r2_train)
- R²を表示。1.0に近いほど「訓練データに対してよく当てはまっている」

サンプルコード⑥ 残差分析
残差分析は、学習済みモデル(回帰直線)の妥当性を評価するために、予測値と実測値の差(残差)を調べる手法です。
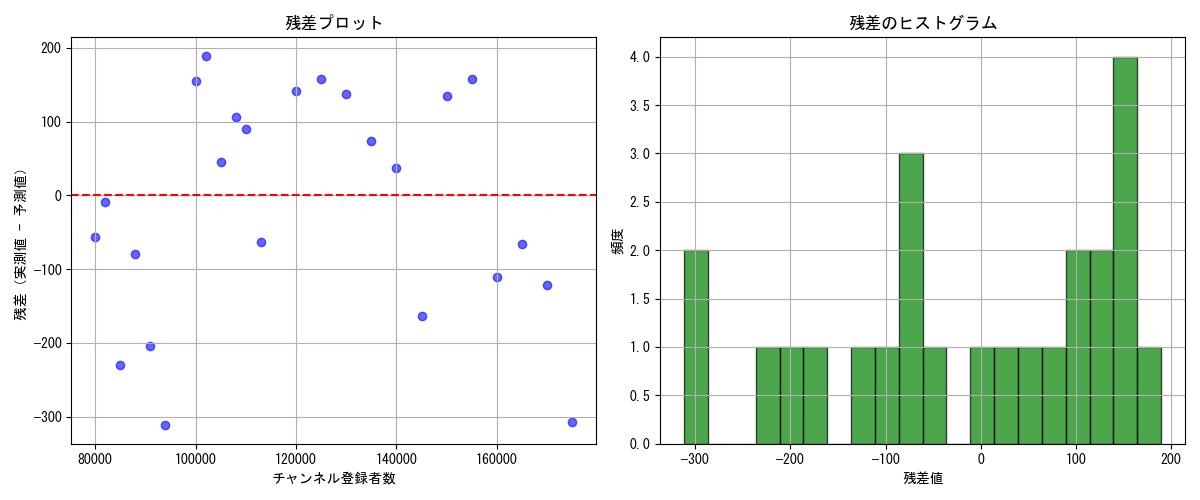
具体的には、求めた残差を使って「残差プロット」や「残差ヒストグラム」を作成して視覚的に確認したり、検定という統計的な手法を用いて数値的に確認したりします。残差分析でチェックする主なポイントは以下のとおりです。
① 残差がX軸全体にランダムに分布しているか? → ランダムに分布していれば、モデルの線形性・等分散性が保たれている
② 特定のパターン(曲線・広がりの変化)がないか? → パターンがあれば、モデルが非線形か、変数変換が必要かも
③ 赤い水平線(y=0)を中心に上下にバラけているか?
【残差ヒストグラムの確認ポイント】
① ヒストグラムが左右対称のベル型になっているか? → ベル型なら残差が正規分布に近い(線形回帰の前提条件を満たす)
② 外れ値(極端な残差)が多すぎないか? → 歪み・尖り・裾が広いと、モデルの見直しやロバスト回帰の検討が必要かも
※正規性検定(Shapiro-Wilk)と合わせて、視覚的に正規分布かどうかを判断する材料になる
残差分析の数理的な内容は以下ページで解説しています。

サンプルコード⑤に「残差分析」の機能を追加したものが以下になります。
| 指標 | 値 | 解釈 |
|---|---|---|
| 残差の平均 | -12.36 | わずかに過大予測傾向(予測値が実測値より高め)。許容範囲。 |
| 残差の標準偏差 | 約151.4 | 残差のばらつきがやや大きい(RMSEより広い) 。fold間でばらつきがある可能性がある。 |
| 統計量 | 0.9232 | 正規性の程度を示す(1に近いほど正規) |
| p値 | 0.0688 | 5%水準(p値 > 0.05)では帰無仮説を棄却できない。線形回帰モデルの前提条件である「モデルの予測誤差(残差)が正規分布(ガウス分布)に従っている」を満たしていると判断できます。 |
| 観点 | 解釈 |
|---|---|
| 線形性 | 残差がランダムに分布 → OK |
| 分布の形状(等分散性) | 残差の広がりがやや右寄り(正の残差が多い) → 実測値 < 予測値が多い(過大予測) |
| 最頻値が +200 付近 | 一部の予測が大きく外れている可能性あり |
| 左右対称性(正規性) | やや右寄りで完全な正規分布ではないが、極端な歪みはない。統計的にはOK(p値 > 0.05) |
| 裾の広がり | -300〜+200 → 誤差の範囲が広く、一部の予測が大きく外れている可能性あり |
総合的に見ると、線形回帰モデルの前提(線形性・等分散性)をおおむね満たしているが、残差のばらつきが広く、一部の予測が大きく外れている(訓練データに大きな外れ値)が含まれている可能性があると判断できます。
コード解説
from scipy.stats import shapiro
- 「from scipy.stats import shapiro」は、Shapiro-Wilk検定で残差の正規性を検証するためにインポートしています。
# 各foldで学習・評価・残差収集
for train_index, test_index in kf.split(X):
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# 評価指標
r2_scores.append(r2_score(y_test, y_pred))
mae_scores.append(mean_absolute_error(y_test, y_pred))
rmse_scores.append(np.sqrt(mean_squared_error(y_test, y_pred)))
# 残差収集
residuals = y_test - y_pred
all_residuals.extend(residuals)
all_x.extend(X_test.flatten())
- データを5分割し、各foldで訓練・予測・評価(R², MAE, RMSE)・残差(実測値 − 予測値)の取得を行っています。
print("残差の平均:", np.mean(residuals_array))
print("残差の標準偏差:", np.std(residuals_array))
- 残差の平均(0に近ければ偏りなし)、標準偏差(小さければ誤差が安定)を計算して表示していmasu.
stat, p_value = shapiro(residuals_array)
...
if p_value > 0.05:
print("→ 正規分布に従う可能性が高い")
- Shapiro-Wilk検定により、残差が正規分布に従うかを調べています。
- p値 > 0.05 → 正規性あり(線形回帰の前提を満たす)
# 残差プロット
plt.figure(figsize=(12, 5))
plt.rcParams["font.family"] = "MS Gothic" # 日本語フォントの設定(Windows環境向け)
plt.subplot(1, 2, 1)
plt.scatter(all_x, residuals_array, color="blue", alpha=0.6)
plt.axhline(y=0, color="red", linestyle="--")
plt.xlabel("チャンネル登録者数")
plt.ylabel("残差(実測値 - 予測値)")
plt.title("残差プロット")
plt.grid(True)
# 残差ヒストグラム
plt.subplot(1, 2, 2)
plt.hist(residuals_array, bins=20, color="green", alpha=0.7, edgecolor="black")
plt.xlabel("残差値")
plt.ylabel("頻度")
plt.title("残差のヒストグラム")
plt.grid(True)
plt.tight_layout()
plt.show()
- 残差の性質を視覚的に評価するために、matplotlibで2種類のプロット**を描画しています。
- 残差プロットでは、特徴量と残差の関係を可視化し、線形性・等分散性の確認を行います。
- 残差ヒストグラムでは、残差の分布から正規性の視覚的確認を行います。
サンプルコード⑦ 汎化性能の検証
汎化性能とは、学習済みモデルが未知のデータに対してどれだけ正確に予測できるかというものです。
つまり、「訓練データ」から作成した回帰直線が、訓練では未使用の新しいデータに対しても有効かどうかを確認します。汎化性能が低い場合は、「過学習対策」を検討する必要があります。汎化性能の検証を行うときの基本的な流れは以下のとおりです。
- 訓練では未使用の新しいデータで構成された「テストデータ」を作成します。
- 例:作り方に決まりはありませんが、元のデータセットから80%を訓練用、20%をテスト用として使うことが多いです。注意点として、訓練用とテスト用は分ける必要があります。
- 「学習済みモデル」に「テストデータ」を入力し、予測を行います。
- 「テストデータ」の特徴量 $x_{\text{test}}$ を学習済みモデルに入力し、予測値 $\hat{y}_{\text{test}}$ を取得します。
- 精度の評価します。
- 実際の値 $y_{\text{test}}$ と予測値 $\hat{y}_{\text{test}}$ を比較し、誤差を計算します。
- 誤差を使って、平均絶対誤差(MAE)、平均二乗誤差(MSE)、MSEの平方根(RMSE)、決定係数$R^2$などの指標を求め、性能を評価します。
- 決定係数は訓練データに対してうまくフィットしているかだけでなく、テストデータに対してうまくフィットしているかの指標にも用いることができます。
| 指標名 | 意味 | 数値の見方 |
|---|---|---|
| MAE (Mean Absolute Error) |
予測値と実測値の「平均的なズレ」、「予測が毎回どれくらい外れるか」 | 小さいほど良い 例:MAE = 300 → 平均300人ズレてる |
| MSE (Mean Squared Error) |
誤差を2乗して平均化(大きな誤差に厳しい) | 小さいほど良い 例:MSE = 90,000 → 誤差の2乗平均が9万 |
| RMSE (Root Mean Squared Error) |
MSEの平方根(単位が元データと同じ)、誤差の平均的な大きさを直感で把握 | 小さいほど良い 例:RMSE = 300 → MAEと同じくらいなら安定 |
| $R^2$(決定係数) | テストデータに対する説明力 | 1に近いほど良い。 |
計算方法など、数理的な内容は以下ページで解説しています。

※読み込んだデータ:dataset01.csv
上記の実行結果を解釈してみます。
| 指標 | 意味 | 今回の値 | 評価 |
|---|---|---|---|
| MAE(平均絶対誤差) | 実測値と予測値の誤差の平均(絶対値) | ≈ 116.7 | 平均で約117人の誤差。誤差が小さく、予測は安定している。 |
| MSE(平均二乗誤差) | 誤差の二乗平均。外れ値に敏感。 | ≈ 15087.6 | 二乗誤差としてはやや大きめだが、外れ値が少なければ許容範囲。 |
| RMSE(平方平均誤差) | MSEの平方根。誤差の「標準的な大きさ」。 | ≈ 122.8 | 1予測あたりの誤差が約123人。MAEと近く、外れ値の影響は少ない。 |
| R²(決定係数) | モデルがどれだけデータを説明できているか(0〜1) | ≈ 0.976 | 97.6%のばらつきを説明できている。非常に高精度なモデル。 |
「訓練データの決定係数R²」と「テストデータの決定係数R²」がともに0.97以上と高いため、学習済みモデルは過学習しておらず、汎化性能も高いだろうと思われます。MAE ≈ 117人、RMSE ≈ 123人 という誤差は、視聴者数のスケール(数千人)を考えると小さいと言えます。また、*MAEとRMSEが近いため、外れ値の影響が少なく、予測が安定していると評価できます。ただし、過学習の可能性やデータの偏り**がないかはさら確認が必要です(例:交差検証や残差分析)。
コード解説
重要な部分を抜粋して解説します。
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.2, random_state=42
)
train_test_split()関数は、特徴量xとターゲット変数yを訓練データ(train)とテストデータ(test)に分割しています。test_size=0.2はデータの20%をテスト用に分割(残り80%が訓練用)する引数です。random_state=42は分割の再現性を保証(毎回同じ分割になる)する引数です。x_train,y_train:モデルの訓練データに使う特徴量とターゲット変数x_test,y_test:モデルの汎化性能を評価するためのテストデータに使う特徴量とターゲット変数
# テストデータに対する予測
y_pred = model.predict(x_test)
# 汎化性能の評価指標を算出
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
r2_pred = r2_score(y_test, y_pred)
mean_absolute_error(y_test, y_pred)関数は、MAE(予測値y_predと実測値y_testの絶対誤差の平均)を計算mean_squared_error(y_test, y_pred)関数は、予測誤差の二乗平均(MSE)を計算。ただし、squared=True(デフォルト)だとMSEを返すが、squared=FalseだとRMSEを返す。np.sqrt(mse)関数は、MSEの平方根を取ってRMSEを計算。r2_score(y_test, y_pred)関数は、決定係数 R² を計算。
サンプルコード⑧ 交差検証
交差検証(Cross Validation)は、モデルの汎化性能(未知データへの強さ)を評価するためのテスト方法の1つです。 データを複数の「訓練用」と「検証用」に分割して、モデルを何度も学習・評価することにより、評価の偏りを平均化し、信頼性を向上させます。
サンプルコード⑥で訓練データとテストデータに分割して性能評価をしていますが、K分割交差検証(K-Fold Cross Validation)を使うことで、より安定した汎化性能の評価が可能になります。
交差検証のやり方はいくつかありますが、今回は代表的な方法である「K分割交差検証(K-Fold Cross Validation)」を行います。
- データを K個のグループ(fold) に分割する
- 各回で、K-1個を訓練用、残り1個を検証用としてモデルを学習・評価する
- これを K回繰り返す(foldを順番に検証用にする)
- 最終的に、K回の評価結果の平均を取る
例えば、K=5 の場合、以下のようになります。
- データを5分割(Fold1〜Fold5)
- 各回で1つのfoldを検証用、残り4つを訓練用に使う
- 5回繰り返して、平均的な性能を評価
| 回 | 訓練データ | 検証データ |
|---|---|---|
| ① | Fold2〜5 | Fold1 |
| ② | Fold1,3〜5 | Fold2 |
| ③ | Fold1,2,4,5 | Fold3 |
| ④ | Fold1〜3,5 | Fold4 |
| ⑤ | Fold1〜4 | Fold5 |
以下は、「K分割交差検証(k=5)」で汎化性能の評価を行うサンプルコードです。
コード解説
from sklearn.model_selection import KFold
- scikit-learn の中から
KFoldクラスをインポートします。 model_selectionモジュールにあるクラスで、 データを K個の等しいサイズのグループ(fold) に分割するためのものです。
kf = KFold(n_splits=5, shuffle=True, random_state=42)
- KFoldクラスで分割方法(foldの作り方)を定義しています。(実際に分割はまだ行っていない)
| 引数 | 意味 | 解説 |
|---|---|---|
n_splits=5 |
分割数(foldの数) | データを5つのグループに分けて、5回の交差検証を行う |
shuffle=True |
データをシャッフルするか | データが時系列順やカテゴリ順に並んでいると、fold間に偏りが出ます。、それを防ぐためにシャッフルをします。 例:登録者数が少ないVTuberが前半に集中していたら、Fold1だけ性能が悪くなる可能性がある |
random_state=42 |
シャッフルの乱数シード | シャッフルの結果を再現可能にする(42はよく使われる定数)。シャッフルは乱数で行われるため、実行するたびに結果が変わる |
# 各評価指標を定義した交差検証で算出
r2_scores = cross_val_score(model, X, y, cv=cv, scoring=make_scorer(r2_score))
mae_scores = cross_val_score(
model, X, y, cv=cv, scoring=make_scorer(mean_absolute_error)
)
mse_scores = cross_val_score(
model, X, y, cv=cv, scoring=make_scorer(mean_squared_error)
)
cvは交差検証(Cross Validation)における「分割方法」を指定する変数です。cross_val_score()やcross_validate()に渡すことで、 データの分割方法(foldの作り方)を指定しています。
サンプルコード⑨ 予測の不確かさ
単回帰分析では、ある特徴量$ x $ に対してターゲット変数 $ y $ を予測する回帰直線を求めますが、その予測値がどれくらい確かなものなのかを知ることが重要です。たとえば、登録者数が20万人のVTuberに対して「視聴者数は約5,656人」と予測できたとしても、
- その予測値はどれくらいの誤差を含んでいるのか?
- 実際の視聴者数はどの範囲に収まりそうか?
- モデルの予測は平均的にどれくらい信頼できるのか?
といった疑問が生じます。こうした予測の不確かさを定量的に評価するために、「信頼区間」や「予測区間」が用いられます。
| 区間 | 意味 | 例(視聴者数の予測) |
|---|---|---|
| 信頼区間(Confidence Interval) | 回帰直線の平均的な予測値がどの範囲にあるかを示す | 「登録者数20万人のVTuberの平均的な視聴者数は、5,600〜5,700人の間にあると考えられる」 |
| 予測区間(Prediction Interval) | 個々のデータ点の実際の視聴者数がどの範囲にあるかを示す | 「登録者数20万人のVTuberの実際の視聴者数は、4,800〜6,400人の間になる可能性がある」 |
「信頼区間」と「予測区間」の数理的な内容は以下ページで解説しています。

以下は、 「信頼区間」と「予測区間」をグラフにプロットするサンプルコードです。
■実行結果
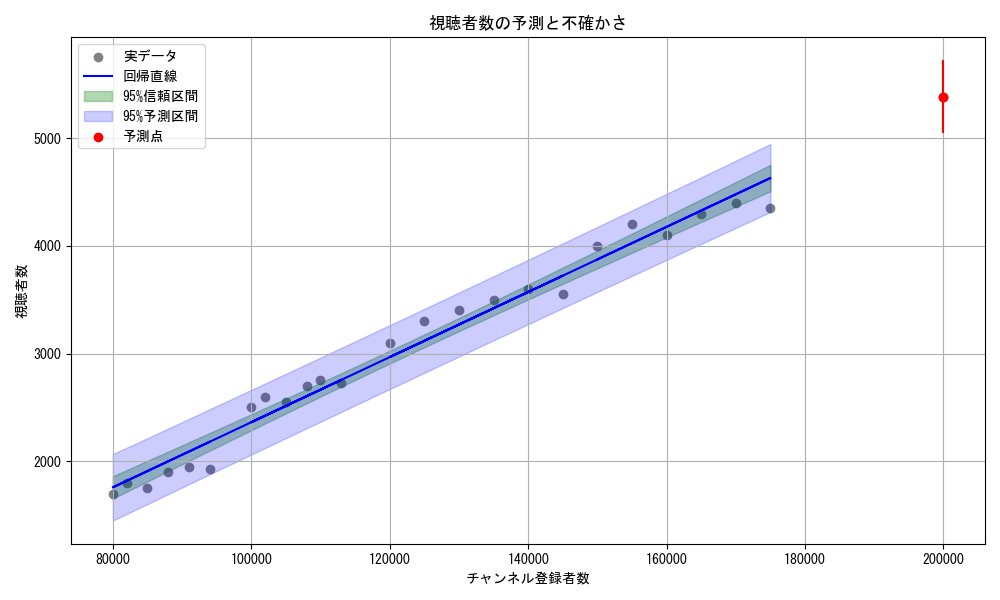
コード解説
from scipy import stats
- Scipy.stats:t分布による区間推定を行うためにインポート
def calc_intervals(model, x_train, x_new, se, confidence=0.95):
x_new = np.array(x_new).flatten()
y_pred = model.predict(x_new.reshape(-1, 1))
n = len(x_train)
x_mean = np.mean(x_train)
Sxx = np.sum((x_train.flatten() - x_mean) ** 2)
t = stats.t.ppf((1 + confidence) / 2, df=n - 2)
# 信頼区間(回帰直線の不確かさ)
se_conf = se * np.sqrt(1 / n + ((x_new - x_mean) ** 2 / Sxx))
conf_lower = y_pred - t * se_conf
conf_upper = y_pred + t * se_conf
# 予測区間(新しい観測値の不確かさ)
se_pred = se * np.sqrt(1 + 1 / n + ((x_new - x_mean) ** 2 / Sxx))
pred_lower = y_pred - t * se_pred
pred_upper = y_pred + t * se_pred
return y_pred, conf_lower, conf_upper, pred_lower, pred_upper
- この関数は、新しい説明変数
x_newに対して以下を計算します。
| 出力 | 意味 |
|---|---|
y_pred |
回帰直線による予測値 |
conf_lower, conf_upper |
信頼区間(平均的な予測値の不確かさ) |
pred_lower, pred_upper |
予測区間(個別の新しい観測値のばらつき) |
Sxx: 説明変数の分散(回帰式の分母)t: t分布の臨界値(95%区間なら約1.96)- se_confは、信頼区間。回帰直線の推定精度(平均値の不確かさ)
- se_predは、予測区間**。新しい観測値のばらつきも含む(個別予測の不確かさ)
residuals = y - y_fit
se = np.sqrt(np.sum(residuals**2) / (len(x) - 2))
- 残差:実測値と予測値の差
- 標準誤差
seは、モデルのばらつきの尺度。区間推定に使います。
x_new = np.array([[200000]])
y_new, conf_lo, conf_hi, pred_lo, pred_hi = calc_intervals(model, x, x_new, se)
x_new: 新しい登録者数(20万人)y_new: 予測視聴者数conf_lo,conf_hi: 信頼区間pred_lo,pred_hi: 予測区間
print(f"傾き a: {model.coef_[0]:.4f}")
print(f"切片 b: {model.intercept_:.2f}")
print(f"予測視聴者数: {float(y_new[0]):.2f}")
print(f"95%信頼区間: [{float(conf_lo[0]):.2f}, {float(conf_hi[0]):.2f}]")
print(f"95%予測区間: [{float(pred_lo[0]):.2f}, {float(pred_hi[0]):.2f}]")
- 回帰式:
y = ax + b - 信頼区間:平均的な予測値の不確かさ
- 予測区間:個別の視聴者数のばらつき
plt.scatter(x, y, ...)
plt.plot(x, y_fit, ...)
x_range = np.linspace(x.min(), x.max(), 100).reshape(-1, 1)
y_range, conf_lo_range, conf_hi_range, pred_lo_range, pred_hi_range = calc_intervals(...)
x_range: 回帰直線と区間を描画するための補間点
plt.fill_between(..., conf_lo_range, conf_hi_range, color="green", alpha=0.3)
plt.fill_between(..., pred_lo_range, pred_hi_range, color="blue", alpha=0.2)
- 信頼区間を緑色で描画(狭い)
- 予測区間を青色で描画(広い)
plt.scatter(x_new, y_new, ...)
plt.errorbar(x_new, y_new, yerr=[下側誤差, 上側誤差], ...)
- 赤点:新しい予測点(20万人)
- 誤差バー:予測区間の上下限
関連ページ


コメント
youtubeからこちらのサイトに来ました。
貴重な情報ありがとうございます。
【Scikit-learn】単回帰分析の所で質問なんですが、
# 説明変数xに “x1″のデータを使用
x = data.loc[:, [‘x1’]].values
# 目的変数yに “x2″のデータを使用
y = data[‘x2’].values
にするとあります。
locでx1のデータを抜き出すのと、x2のデータではデータの型が違うのですか?
どちらもSeries型となって、valuesでnumpy配列にしていると思うのですが。
xが2次元配列、yが1次元配列というところまで勉強している程度なんで、
基礎的な質問で申し訳ないですが、どのような意図でこのようにしているのか教えて下さい。
fit()にXとyを代入する際、説明変数Xは行列(2次元配列)を与える必要があります。
data[‘x2’].valuesだと、1次元配列として1つの配列を取得するため、二次元配列に変換してやるコードを追加する必要があります。
その手間を省く意味と、重回帰の場合はlocを使わないといけないという理由でdata.loc(複数のカラムを2次元配列で取得)としています。
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
fit(self, X, y, sample_weight=None)[source] X{array-like, sparse matrix} of shape (n_samples, n_features) Training data yarray-like of shape (n_samples,) or (n_samples, n_targets) Target values. Will be cast to X’s dtype if necessary