この記事では、Python言語を用いて、2リンクマニピュレータ(2自由度アーム)の逆運動学を収束計算で求め、シミュレーションする方法をソースコード付きで解説します。
逆運動学の計算(収束計算)
ロボットアームの構造が複雑になると数式で逆運動学が解けなくなります。
そのような場合は、収束計算を用いて解を求めます。
| – | 収束計算の流れ |
|---|---|
| 1 | 仮の解(初期関節角度)を設定する |
| 2 | 仮の解から順運動学を用いて手先位置を求める |
| 3 | 目標位置と手先位置の誤差から仮の解を微修正する |
| 4 | 位置誤差が十分小さくなるまで1~3を繰り返す |
逆運動学の計算プログラム(数値計算)
Pythonを用いて収束計算で逆運動学を解き、姿勢を描画するプログラムを作成しました。
| – | プログラムの処理手順 |
|---|---|
| 1 | 2リンクアームのパラメータ(リンクの長さ、初期関節角度)を設定する |
| 2 | 手先の目標位置を設定する |
| 3 | 逆運動学を収束演算で計算し,目標位置を達成するための関節角度を導出する |
| 4 | 計算結果からアームの姿勢を表示する |
ソースコード
サンプルプログラムのソースコードです。
# -*- coding: utf-8 -*-
import numpy as np
from numpy import sin,cos
import matplotlib.pyplot as plt
# 並進行列(x軸方向に並進)
def L(l):
Li = np.matrix((
( 1., 0., l),
( 0., 1., 0.),
( 0., 0., 1.)
));
return Li
# 回転行列(z軸周りに回転)
def Rz(th):
R = np.matrix((
(cos(th), -sin(th), 0.),
(sin(th), cos(th), 0.),
(0., 0., 1.)
))
return R
# 座標変換行列の微係数(z軸周り)
def dRz(th):
dR = np.matrix( (
(-sin(th),-cos(th),0.),
( cos(th),-sin(th),0.),
(0.,0.,0.)
));
return dR
# グラフの描画
def plot(x, y):
fn = "Times New Roman"
# グラフ表示の設定
fig = plt.figure()
ax = fig.add_subplot(111, axisbg="w")
ax.tick_params(labelsize=13) # 軸のフォントサイズ
plt.xlabel("$x [m]$", fontsize=20, fontname=fn)
plt.ylabel("$y [m]$", fontsize=20, fontname=fn)
plt.plot(x, y,"-g",lw=5,label="link") # リンクの描画
plt.plot(x, y,"or",lw=5, ms=10,label="joint") # 関節の描画
plt.xlim(-1.2,1.2)
plt.ylim(-1.2,1.2)
plt.grid()
plt.legend(fontsize=20) # 凡例
plt.show()
def arm2_ik(X, L, th):
[x, y] = X
[l1, l2] = L
[th1, th2] = th
X = np.matrix(( ( np.array(x) ), ( np.array(y) ) ))
th1 = np.radians(th1) # 仮りの解1
th2 = np.radians(th2) # 仮りの解2
# 収束計算を50回繰り返す
for j in range(50):
# 原点座標(縦ベクトル)
x = np.array([[0.],[0.],[1.]] )
P = np.matrix((
(1.,0.,0.),
(0.,1.,0.),
))
# 現在の手先位置を求める
Xg = P * Rz(th1) * L(l1) * Rz(th2) * L(l2) * x
# ヤコビ行列を求める
J1 = dRz(th1) * L(l1) * x
J2 = Rz(th1) * L(l1) * dRz(th2) * L(l2) * x
JJ = np.c_[J1,J2] # 3つの列ベクトルを連結する
J = P * JJ #ヤコビ行列
invJ = J.T * np.linalg.inv(J * J.T) #ヤコビ行列の逆行列
dx = X - Xg #位置の変位量
th = 0.1 * invJ * dx #逆運動学の式
th1 = th1 + th[0,0]
th2 = th2 + th[1,0]
return th1, th2
# 順運動学の計算
def arm2_fk(L, th):
[l1, l2] = L
[th1, th2] = th
vec = np.array([[0.],[0.],[1.]] )
(x1, y1, z1) = Rz(th1) * L(l1) * vec # 第1関節の位置
(x2, y2, z2) = Rz(th1) * L(l1) * Rz(th2) * L(l2) * vec # 第2関節の位置
return x1, y1, x2, y2
# メイン
def main():
# パラメータ
L = [0.5, 0.5] # リンク1, 2の長さ
X = [0.5, 0.5] # 手先の目標位置(x,y)
th = [20, 20] # 初期関節角度(仮の解)
# 逆運動学の計算
th = arm2_ik(X, L, th)
# 順運動学の計算
(x1, y1, x2, y2) = arm2_fk(L, th)
# ロボットアームの描画
x = (0, x1, x2)
y = (0, y1, y2)
plot(x, y)
if __name__ == '__main__':
main()
実行結果
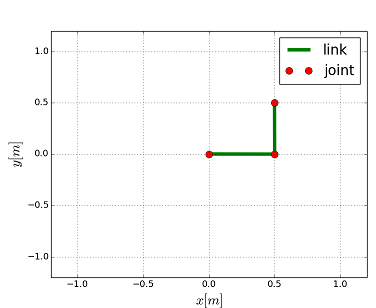
サンプルプログラムの実行結果です。
リンク1、2の長さが0.5で手先の目標位置(0.5, 0.5)で計算した結果です。
| – | 関連ページ |
|---|---|
| 1 | ■Pythonでロボットシミュレーション |
| 2 | ■ロボット工学入門 基礎編 |
| 3 | ■Python入門 サンプル集 |
| 4 | ■NumPy入門 サンプル集 |

コメント