Python版OpenCVとNumPyを用いてフーリエ変換とローパスフィルタを実装し、画像からノイズを除去する方法をソースコード付きで解説します。
フーリエ変換とは
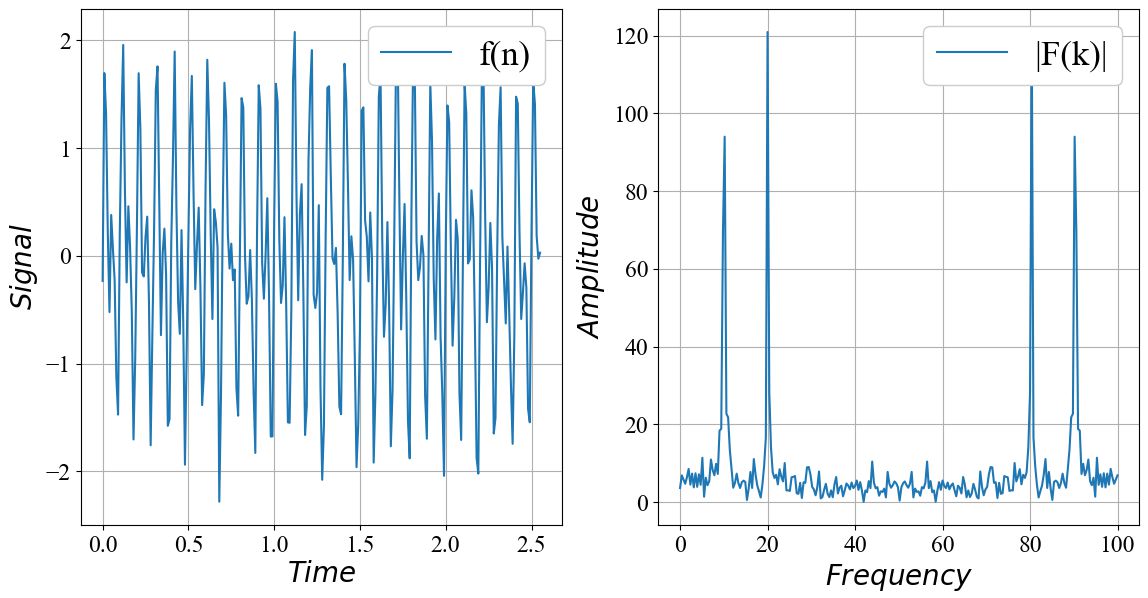
フーリエ変換(Fourier Transform)とは、信号を時間領域から周波数領域に変換する処理です。
フーリエ変換では「一定の周期をもつ信号は複数の正弦波の和で表現できる」というフーリエ級数の性質を使って、周波数領域に変換します。
これにより、信号に「どのような周波数成分がどれだけ含まれているのか」を解析することができます。
変換後の信号、正弦波の和は$sin(wt)$でなく、複素正弦波$e^{jwt}$を使うため、複素数で表現されます。
逆に、周波数領域に一度変換された信号を時間領域に戻すこともできます。
これを逆フーリエ変換(Inverse Fourier Transform)といいます。フーリエ変換の詳細については以下ページで解説しています。
解説動画
本ページの内容は以下動画でも解説しています。
画像処理におけるフーリエ変換
フーリエ変換は周波数解析ができる便利なデータ変換です。
画像に対しても利用できますが、周波数の考え方が通常の信号とは異なるので注意する必要があります。
- 通常の信号データ
- 周波数=単位時間内にどのくらい振動するか
- 画像データ
- 周波数=単位ピクセル内に画素値がどのくらい変化するか
よって、画像データの周波数は1[px]移動したときの画素値の変化が激しいほど高周波となります。画像処理でのフーリエ変換は「時間領域→周波数領域」ではなく「空間領域→空間周波数領域」となります。
また、画像は2次元データであり、水平方向と垂直方向の2つの空間周波数成分を持っています。
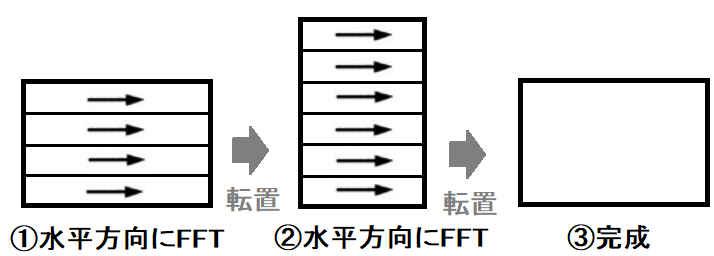
そのため、画像を空間領域から空間周波数領域に変換するには、以下のようにフーリエ変換を2回行います。
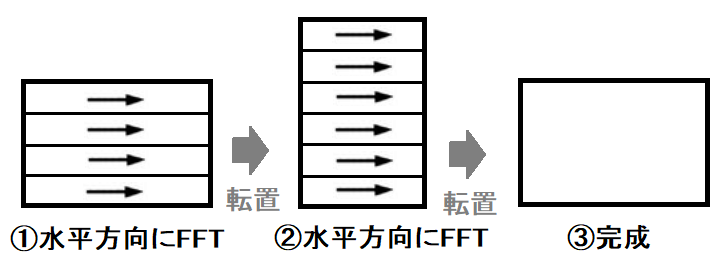
①画像に対して水平方向にフーリエ変換を行います。
②画像を転置し、再び水平方向にフーリエ変換を行います。
③もう1度画像を転置すれば完成です。
(結果的に画像データに対して水平方向と垂直方向にフーリエ変換を行うことになります)
実際にフーリエ変換を行う際は、高速フーリエ変換(FFT)を用います。
ただし、高速フーリエ変換を利用するには画像の縦横の画素数[px]が2の冪乗である必要があります。
画像の振幅スペクトル
画像を空間周波数領域に変換すると、次のような振幅スペクトルが得られます。
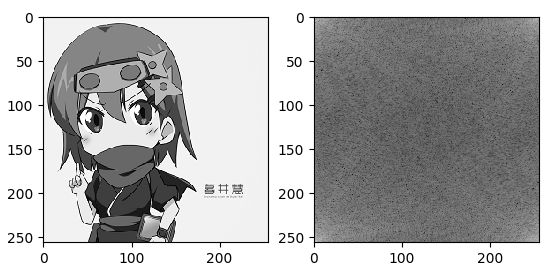
※プロ生ちゃんの画像をお借りして入力しました。
この振幅スペクトルは、中心から離れるに従って低周波数成分になるスペクトルで、画像データの周波数分布を表します。
画素値が大きい(白っぽい)ほど、その周波数成分が多く含まれていることになります。
つまり、中心付近に白い画素が集中するほど画像に高周波成分が多く含まれることを意味します。
(逆に、四隅付近に集中すれば低周波数成分が多く含まれる)
このように画像の振幅スペクトルからも(空間)周波数成分の解析ができます。
空間周波数領域の入れ替え
振幅スペクトルを利用する場合、第1象限と第3象限、第2象限と第4象限を入れ替えて利用するのが一般的です。
その際、中心から離れるに従って高周波数成分となるスペクトルへ変換されます。
入れ替えにより、後述する空間周波数フィルタリングを簡単に行うことができるようになります。
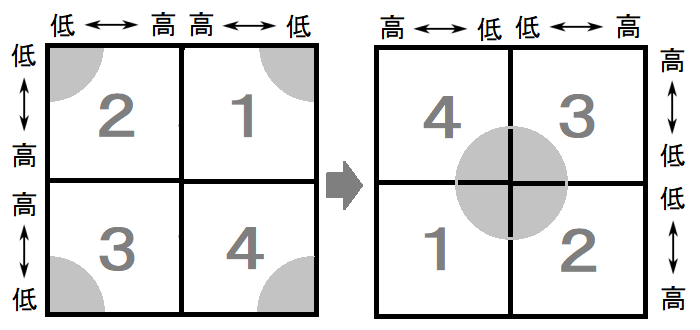
■入れ替えた例
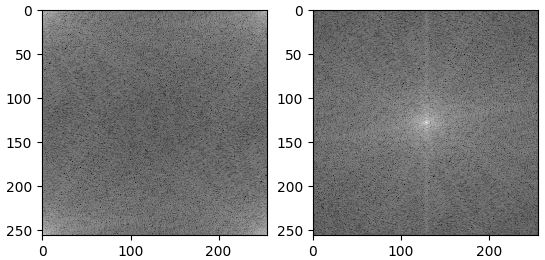
空間周波数フィルタリング
空間周波数フィルタリングでは、画像から特定の周波数成分のみを取り出します。
代表的なものは「ローパスフィルタ」「ハイパスフィルタ」「バンドパスフィルタ」です。
- ローパスフィルタ
- 低周波数成分のみを通過させるフィルタ
- 画像のノイズ除去など
- ハイパスフィルタ
- 高周波成分のみを通過させるフィルタ
- 画像の輪郭、特徴点抽出など
- バンドパスフィルタ
- 特定範囲の周波数成分のみを通過させるフィルタ
- 画像のデータ圧縮など(見た目の影響が少ない成分を除去)
空間周波数フィルタの設計例と操作手順
周波数領域の象限を入れ替えることで次のように空間周波数フィルタリングを簡単に行うことができます。
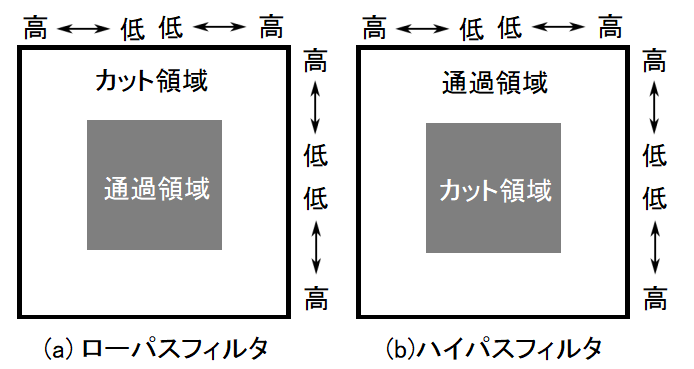
ローパスフィルタ(a)では、中心付近にある低周波数成分のみを通過させます。
一方、ハイパスフィルタ(b)では端の方にある高周波数成分のみを通過させます。
プログラムで実装する場合、カットする領域のスペクトルのみを0にします。
空間周波数フィルタリングの基本的な操作手順は次の通りです。
- 画像に対してフーリエ変換を行い、空間周波数領域に変換します。
- 空間周波数領域の象限を入れ替えます。
- フィルタリングを行います。(例えば、ローパスフィルタならカット領域のスペクトルを0にします)
- 周波数領域の象限を元に戻します。
- 画像に対して逆フーリエ変換を行い、空間領域に戻します。
ローパスフィルタとは、その名の通り、信号の低周波数成分のみを通過させます。
画像データの場合は、画素値の変化が小さい部分が低周波成分となります。(ノイズは高周波成分)
つまり、画像処理においてはローパスフィルタでノイズ除去などに利用できます。原理の詳細は以下ページで解説しています。
ローパスフィルタの実装
今回は、Python+OpenCVを用いて画像のノイズ除去を行うためのローパスフィルタを作成します。
大まかな処理手順は以下のようになります。
①高速フーリエ変換で画像データを空間領域から空間周波数領域に変換します。
②零周波数成分を中心に移動します。(空間周波数領域の中心ほど低周波数成分)
③ハイパスフィルタで高周波成分のみを取り出します。(空間周波数領域の中心のデータは0に置換)
③高速逆フーリエ変換でデータを空間領域に戻します。
サンプルコード① ローパスフィルタでノイズ除去
サンプルプログラムのソースコードです。
実行結果
サンプルプログラムの実行結果です。入力画像は私がスマート望遠鏡「SeeStar S50」で撮影した天体写真(M42、オリオン大星雲)です。
■入力画像(左)と出力画像(右)


一部分を拡大すると以下のとおりです。ノイズが低減(平滑化)されていることがわかります。
■入力画像(左)と出力画像(右)


コード解説
上記サンプルコードのポイントを解説します。
以下の関数で、ローパスフィルタの処理を定義しています。
def lowpass_filter(src, param = 0.5):
# 高速フーリエ変換(2次元)
src = np.fft.fft2(src)
# 画像サイズ
height, width = src.shape
# 画像の中心座標
cy, cx = int(height/2), int(width/2)
# フィルタのサイズ(矩形の高さと幅)
rh, rw = int(param*cy), int(param*cx)
# 第1象限と第3象限、第1象限と第4象限を入れ替え
fsrc = np.fft.fftshift(src)
# 入力画像と同じサイズで値0の配列を生成
fdst = np.zeros(src.shape, dtype=complex)
# 中心部分の値だけ代入(中心部分以外は0のまま)
fdst[cy-rh:cy+rh, cx-rw:cx+rw] = fsrc[cy-rh:cy+rh, cx-rw:cx+rw]
# 第1象限と第3象限、第1象限と第4象限を入れ替え(元に戻す)
fdst = np.fft.fftshift(fdst)
# 高速逆フーリエ変換
dst = np.fft.ifft2(fdst)
# 実部の値のみを取り出し、符号なし整数型に変換して返す
return np.uint8(dst.real)
メイン関数内の以下の部分で、読み込んだ画像データを画像をRGBの各チャンネルに分割し、各チャンネルに対してローパスフィルタを適用し、フィルタ処理後の各チャンネルを再度結合しています。
# RGB画像をRed, Green, Blueの1チャンネル画像に分割
img_blue, img_green, img_red = cv2.split(img)
# ローパスフィルタ処理
himg_blue = lowpass_filter(img_blue, param)
himg_green = lowpass_filter(img_green, param)
himg_red = lowpass_filter(img_red, param)
# RGB画像に戻す
himg = cv2.merge((himg_blue, himg_green, himg_red))
サンプルコード② ローパスフィルタでノイズ除去(改良版)
サンプルコード①を改良し、ガウス分布で高周波になるほどノイズ除去を強く行うようにします。
これでより自然にノイズ除去を行うことができます。
以下は、サンプルプログラムのソースコードです。
実行結果
サンプルプログラムの実行結果です。
■入力画像(左)と出力画像(右)


入力画像、サンプルコード①、サンプルコード②の実行結果を拡大して比較してみます。
■入力画像(左)、サンプルコード①の出力画像(中央)、サンプルコード②の出力画像(右)



サンプルコード①の出力画像は全体的にぼかしが強くなっています。
つまり、サンプルコード②の方がサンプルコード①よりも自然にノイズ除去できていることがわかります。
コード解説
サンプルコード②のポイントを解説します。
# ガウス分布のマスクを生成
y, x = np.ogrid[:height, :width]
mask = np.exp(-((x - cx)**2 + (y - cy)**2) / (2 * (sigma * min(height, width) / 2)**2))
上記では、ガウス分布を用いてフィルタのマスクを作成しています。このマスクは、周波数領域において中心から遠い位置にある成分(高周波数成分)を減少させます。
np.ogrid[:height, :width]のogridは、「open grid」の略で、数値の配列を生成します。ここでは、画像の高さ(height)と幅(width)に基づいて、座標軸を作成します。
cxとcyは画像の中心の座標、(x - cx)**2は各画素の横方向の距離の2乗を計算し、(y - cy)**2は縦方向の距離の2乗を計算します。距離の2乗を合計し、ガウス分布の式に基づいて、画像の中心からの距離が大きくなるにつれて、値が指数的に減少します。
# ガウス分布でフィルタリング(高周波成分ほど値を小さくする)
fdst = fsrc * mask
生成したマスクを用いてフーリエ変換された画像(fsrc)を上記部分でフィルタリングします。
fsrcはフーリエ変換された画像です。maskは先ほど生成したガウス分布のマスクです。
画像の各画素に対して、ガウス分布のマスクを掛けることで、画像の高周波成分を減少させます。中心に近い低周波成分はほとんど影響を受けず、中心から遠い高周波成分は大幅に減少されます。
この処理により、画像のノイズをより自然に除去することができます。
おすすめ記事




コメント